Example of Bootstrapping
Example of Bootstrapping
This example uses the Car Physical Data.jmp sample data table. A tire manufacturer wants to predict an engine’s horsepower from the engine’s displacement (in3). The company is most interested in estimating the slope of the relationship between the variables. The slope values help the company predict the corresponding change in horsepower when the displacement changes.
In this example, the regression assumption of homogeneity of variance is violated, so the confidence limits from the regression analysis for the slope might be misleading. For this reason, the company uses a bootstrap estimate of the confidence interval for the slope.
1. Select Help > Sample Data Library and open Car Physical Data.jmp.
2. Select Analyze > Fit Y by X.
3. Select Horsepower and click Y, Response.
4. Select Displacement and click X, Factor.
5. Click OK.
6. Click the red triangle next to Bivariate Fit of Horsepower By Displacement and select Fit Line.
The slope estimate is 0.503787, approximately 0.504.
7. (Optional) Right-click in the Parameter Estimates report and select Columns > Lower 95%.
8. (Optional) Right-click in the Parameter Estimates report and select Columns > Upper 95%.
The confidence limits from the regression analysis for the slope are 0.4249038 and 0.5826711.
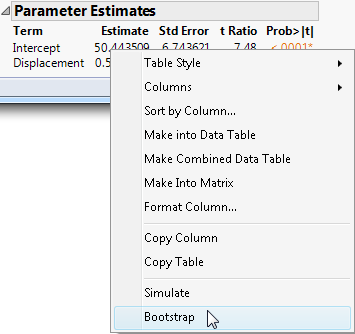
9. Right-click the Estimate column in the Parameter Estimates report and select Bootstrap.
Figure 11.2 The Bootstrap Option
The column that you right-click is relevant when the Split Selected Column option is selected. See Bootstrapping Window Options.
10. Type 1000 for the Number of Bootstrap Samples.
11. (Optional) To match the results in Figure 11.3, type 12345 for the Random Seed.
12. Click OK.
The bootstrap process runs and produces a Bootstrap Results data table with unstacked results for the slope and intercept.
Next, analyze the bootstrapped slope.
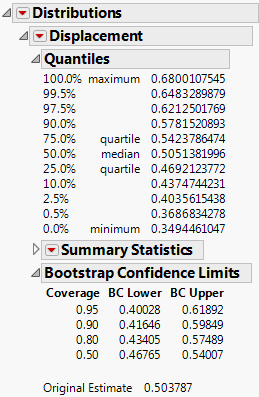
13. In the Bootstrap Results table, run the Distribution script.
The Distribution report includes the Bootstrap Confidence Limits report.
Figure 11.3 Bootstrap Report
The estimate of the slope (step 6) is 0.504. Based on the bootstrap results for 95% coverage, the company can estimate the slope to be between 0.40028 and 0.61892. When the displacement is changed by one unit, with 95% confidence, the horsepower changes by some amount between 0.40028 and 0.61892. The bootstrap confidence interval for the slope (0.400 to 0.619) is slightly wider than the confidence interval (0.425 to 0.583) obtained using the usual regression assumptions in step 7 and step 8.
Note: The BC Lower and BC Upper columns in the Bootstrap Confidence Limits report refer to bias-corrected intervals. See Bias-Corrected Percentile Intervals.