Indicator Parameterization Estimates
This option displays the Indicator Function Parameterization report, which gives parameter estimates for the model where nominal columns are coded using indicator (SAS GLM) parameterization and are treated as continuous. Ordinal columns remain coded using the usual JMP coding scheme. The SAS GLM and JMP coding schemes are described in The Factor Models.
In the JMP coding scheme, the estimate that corresponds to the indicator for a level of a nominal variable is an estimate of the difference between the mean response at that level and the mean response over all the levels. To see the JMP coding, select Save Columns > Save Coding Table from the Standard Least Squares red triangle menu.
In the indicator coding scheme, the estimate that corresponds to the indicator for a level of a nominal variable is an estimate of the difference between the mean response at that level and the mean response at the last level. The last level is the level with the highest value order coding; it is the level whose indicator function is not included in the model.
Caution: Standard errors and t-ratios given in the Indicator Function Parameterization report differ from those in the Parameter Estimates report. This is because the estimates are estimating different parameters.
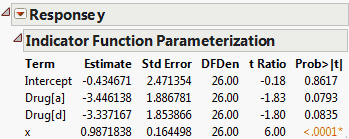
To create the report in Figure 3.24, follow the steps in Example of an Expanded Estimates Report. But instead of selecting Expanded Estimates, select Indicator Parameterization Estimates.
Figure 3.24 Indicator Parameterization Estimates
The JMP coding scheme is used for nominal variables throughout JMP with the exception of the Generalized Regression personality of Fit Model. For more information about the coding scheme for nominal variables in the Generalized Regression personality, see Launch the Generalized Regression Personality.
Note that there might be differences in models derived using the JMP versus the SAS GLM parameterization. Some models are equivalent. Other models (such as no-intercept models, models with missing cells, models with nominal or ordinal effects, and mixture models) might show differences.