Restricted Maximum Likelihood (REML) Method
Based on the fitting method selected, the Fit Least Squares report provides different analysis results and provide additional menu options for Save Columns and Profiler. In particular, the analysis of variance report is not shown because variances and degrees of freedom do not partition in the usual way. You can obtain the residual variance estimate from the REML Variance Component Estimates report. See REML Variance Component Estimates. The Effect Tests report is replaced by the Fixed Effect Tests report where fixed effects are tested. Additional reports give predicted values for the random effects and details about the variance components.
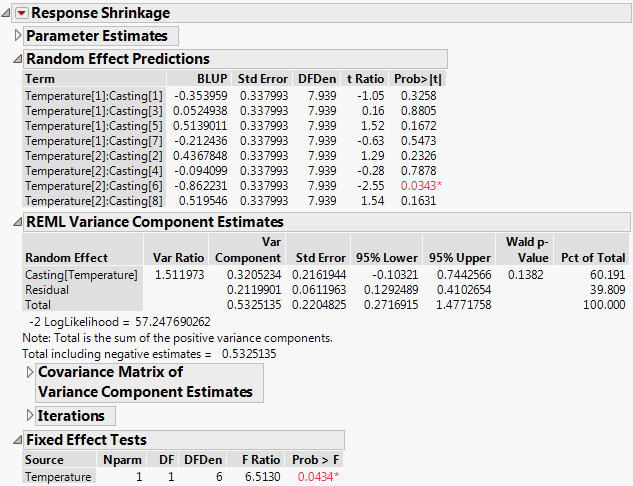
Figure 3.62 shows the report obtained for a fit to the Investment Castings.jmp sample data using the REML method. Run the script Model - REML, and then fit the model. Note that Casting is a random effect and is nested within Temperature.
Figure 3.62 Fit Least Squares Report for REML Method
Random Effect Predictions
For each term in the model, this report gives an empirical estimate of its best linear unbiased predictor (BLUP) and a test for whether the corresponding coefficient is zero.
Note: The Regression Reports > Parameter Estimates option must be selected for the Random Effect Predictions report to appear.
Term
The terms in the model that correspond to random effects.
BLUP
The empirical estimate of the best linear unbiased predictor (BLUP) for each random effect. See Best Linear Unbiased Predictors.
Std Error
The standard error of the BLUP.
DFDen
The denominator degrees of freedom for a test that the effect is zero. In most cases, the degrees of freedom for the t test is fractional.
t Ratio
The t ratio for testing that the effect is zero. The t ratio is obtained by dividing the BLUP by its standard error.
Prob>|t|
The p-value for the test.
Lower 95%
The lower 95% confidence limit for the BLUP. This column appears only if you have the Regression Reports > Show All Confidence Intervals option selected or if you right-click in the report and select Columns > Lower 95%.
Upper 95%
The upper 95% confidence limit for the BLUP. This column appears only if you have the Regression Reports > Show All Confidence Intervals option selected or if you right-click in the report and select Columns > Upper 95%.
Best Linear Unbiased Predictors
The term best linear unbiased predictor (BLUP) refers to an estimator of a random effect. Specifically, it is an estimator that, among all unbiased estimators, minimizes mean square prediction error. The Random Effect Predictions report gives estimates of the BLUPs, or empirical BLUPs. These are empirical because the BLUPs depend on the values of the variance components, which are unknown. The estimated values of the variance components are substituted into the formulas for the BLUPs, resulting in the estimates shown in the report.
REML Variance Component Estimates
When REML is selected as the fitting method in the Fit Model launch window, the REML Variance Component Estimates report is provided. This report contains the following columns:
Random Effect
The random effects in the model.
Var Ratio
The ratio of the variance component for the effect to the variance component for the residual. It compares the effect’s estimated variance to the model’s estimated error variance.
Var Component
The estimated variance component for the effect. Note that the variance component for the Total is the sum of the positive variance components only. The sum of all variance components is given beneath the table.
Std Error
The standard error for the variance component estimate.
95% Lower
The lower 95% confidence limit for the variance component. See Confidence Intervals for Variance Components.
95% Upper
The upper 95% confidence limit for the variance component. See Confidence Intervals for Variance Components.
Wald p-Value
The p-value for the test that the covariance parameter is equal to zero. This column appears only when you have selected Unbounded Variance Components in the Fit Model launch window.
Pct of Total
The ratio of the variance component for the effect to the variance component for the total as a percentage.
Sqrt Variance Component
The square root of the corresponding variance component. It is an estimate of the standard deviation for the effect. This column appears only if you right-click in the report and select Columns > Sqrt Variance Component.
CV
The coefficient of variation for the variance component. It is 100 times the square root of the variance component, divided by the mean response. This column appears only if you right-click in the report and select Columns > CV.
Norm KHC
The Kackar-Harville correction. See Kackar-Harville Correction. This column appears only if you right-click in the report and select Columns > Norm KHC.
Confidence Intervals for Variance Components
The method used to calculate the confidence limits depends on whether you have selected Unbounded Variance Components in the Fit Model launch window. Note that Unbounded Variance Components is selected by default.
• If Unbounded Variance Components is selected, Wald-based confidence intervals are computed. These are valid asymptotically but note that they can be unreliable with small samples.
• If Unbounded Variance Components is not selected, meaning that parameters have a lower boundary constraint of zero, a Satterthwaite approximation is used (Satterthwaite 1946).
Kackar-Harville Correction
In the REML method, the standard errors of the fixed effects are estimated using estimates of the variance components. However, if variability in these estimates is not taken into account, the standard error is underestimated. To account for the increased variability, the covariance matrix of the fixed effects is adjusted using the Kackar-Harville correction (Kackar and Harville 1984; Kenward and Roger 1997). All calculations that involve the covariance matrix of the fixed effects use this correction. These include least squares means, fixed effect tests, confidence intervals, and prediction variances. For statistical details, see The Kackar-Harville Correction.
Norm KHC is the Frobenius (matrix) norm of the Kackar-Harville correction. In cases where the design is fairly well balanced, Norm KHC tends to be small.
Covariance Matrix of Variance Components Estimates
This report gives an estimate of the asymptotic covariance matrix for the variance components. It is the inverse of the observed Fisher information matrix.
Iterations
The estimates of σ2 and the variance components in G are obtained by maximizing a residual log-likelihood function that depends on only these parameters. An iterative procedure attempts to maximize the residual log-likelihood function, or equivalently, to minimize twice the negative of the residual log-likelihood (–2LogLike). The Iterations report provides details about this procedure.
Iter
Iteration number.
-2LogLike
Twice the negative log-likelihood. It is the objective function. See Likelihood, AICc, and BIC.
Norm Gradient
The norm of the gradient (first derivative) of the objective function
Parameters
The column labeled Parameters and the remaining columns each correspond to a random effect. The order of the columns follows the order in which random effects are listed in the REML Variance Component Estimates report. At each iteration, the value in the column is the estimate of the variance component at that point.
The convergence criterion is based on the gradient, with a default tolerance of 10-8. You can change the criterion in the Fit Model launch window by selecting the option Convergence Settings > Convergence Limit and specifying the desired tolerance.
Fixed Effect Tests
When REML is used, the Effect Tests report provides tests for the fixed effects. This report contains the following columns:
Source
The fixed effects in the model.
Nparm
The number of parameters associated with the effect.
DF
The degrees of freedom associated with the effect.
DFDen
The denominator degrees of freedom. These are based on an approximation to the distribution of the statistic obtained when the covariance matrix is adjusted using the Kenward-Roger correction. See Kackar-Harville Correction and Random Effects.
FRatio
The computed F ratio.
Prob > F
The p-value for the effect test.
REML Save Columns Options
When you use the REML method, six additional options appear in the Save Columns menu. These option names start with the adjective Conditional. This prefix indicates that the calculations for these columns use the predicted values for the terms associated with the random effects, rather than their expected values of zero.
Conditional Pred Formula
Saves the prediction formula to a new column in the data table.
Conditional Pred Values
Saves the predicted values to a new column in the data table.
Conditional Residuals
Saves the residuals to a new column in the data table.
Conditional Mean CI
Saves the confidence interval for the mean.
Conditional Indiv CI
Saves the confidence interval for individuals.
 Publish Conditional Formula
Publish Conditional Formula
Creates a conditional prediction formula and saves it as a formula column script in the Formula Depot platform. If a Formula Depot report is not open, this option creates a Formula Depot report. See Formula Depot in Predictive and Specialized Modeling.
REML Profiler Option
When you use the REML method and select Factor Profiling > Profiler, a new option, Conditional Predictions, appears on the red triangle menu next to Prediction Profiler. Note that the conditional values use the predicted values for the random effects, rather than their zero expected values.
Note: The profiler displays conditional predicted values and conditional mean confidence intervals for all combinations of factors levels. Some of these combinations might not be meaningful due to nesting.