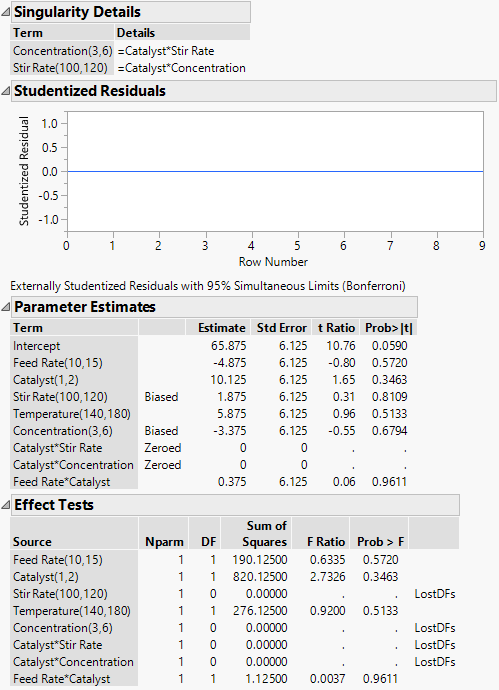
Singularity Details
The linear regression model is formulated as Y = Xβ + ε. Here X is a matrix whose first column consists of 1s, and whose remaining columns are the values of the non-intercept terms in the model. If the model consists of p terms, including the intercept, then X is an n by p matrix, where n is the number of observations. The parameter estimates, denoted by the vector b, are typically given by the formula:
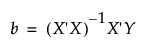
However, this formula presumes that X′X−1 exists, in other words, that the p × p matrix X′X is invertible, or equivalently, of full rank. Situations often arise when X′X is not invertible because there are linear dependencies among the columns of X.
In such cases, the matrix X′X is singular, and the Fit Least Squares report contains the Singularity Details report. This report contains a table of expressions that describe the linear dependencies. The terms involved in these linear dependencies are aliased (confounded).
Figure 3.64 shows reports for the Reactor 8 Runs.jmp sample data table. To obtain these reports, fit a model with Percent Reacted as Y. Enter Feed Rate, Catalyst, Stir Rate, Temperature, Concentration, Catalyst*Stir Rate, Catalyst*Concentration, and Feed Rate*Catalyst as model effects.
Figure 3.64 Singularity and Parameter Estimates Report for Model with Linear Dependencies