Confidence Interval for Two Independent Sample Means
Use the Confidence Interval for Two Independent Sample Means Explorer to determine a sample size for a confidence interval. Select DOE > Sample Size Explorers > Confidence Intervals > Confidence Interval for Two Independent Sample Means. Explore the trade-offs between variability assumptions, sample size, significance, and the margin of error for your interval.
Interval Explorer for Two Independent Sample Means Settings
Set study assumptions and explore sample sizes by using the radio buttons, text boxes, and menus. The profiler updates as you make changes to the settings. Alternatively, you can change the settings by dragging the cross hairs on the profiler curves.
Interval Type
Specifies the type of interval. Specify Bound for a one-sided interval. Specify Interval for a two-sided interval.
Confidence Level
Specifies the confidence level, 1 - alpha.
Population Standard Deviation Assumption
Specifies the distribution for calculations.
Yes
Specifies known group standard deviations, calculations use the z distribution.
No
Specifies unknown group standard deviations, calculations use the t distribution.
Interval Explorer for Two Independent Sample Means Profiler
The profiler enables you to visualize the impact of sample size assumptions on the margin of error calculations. Interactive profiler changes to the sample sizes or standard deviations update the calculated power. Interactive changes to the profiler power update the sample sizes. To solve for a specific variable, use the target variable setting and click Go.
Target Variable
Enables you to solve for a sample size or a standard deviation.
Margin of Error
Specifies the half-width of the interval or the width of a one-sided interval. With all other parameters fixed, margin of error decreases as sample size increases.
Ratio of Group 2 to Group 1 Sample Size
Specifies the ratio between group sample sizes. For equal group sample sizes, set to one.
Note: The ratio can shift as you explore changes to the assumptions due to the mathematical search routines.
Total Sample Size
Specifies the total number of observations (runs, experimental units, or samples) that are needed for your experiment.
Group 1 Sample Size
Specifies the number of observations (runs, experimental units, or samples) that are needed for Group 1 in your experiment.
Group 2 Sample Size
Note: Specifies the number of observations (runs, experimental units, or samples) that are needed for Group 2 in your experiment.
Note: Adjusting the total sample size adjusts the sample size in each group according to the ratio of sample size setting. Adjusting the sample size for one group adjusts the sample size in the other group holding the total sample size fixed.
Group 1 Std Dev (Noise)
Specifies the assumed standard deviation for one of your groups, Group 1.
Group 2 Std Dev (Noise)
Specifies the assumed standard deviation for the second group, Group 2.
Interval Explorer for Two Independent Sample Means Options
The Explorer red triangle menu and report buttons provide additional options:
Simulate Data
Opens a data table of simulated data that are based on the explorer settings. View the simulated response column formula for the settings that are used. Run the table script to analyze the simulated data.
Make Data Collection Table
Creates a new data table that you can use for data collection. The table includes scripts to facilitate data analysis.
Remember Settings
Saves the current settings to the Remembered Settings table. This enables you to save a set of alternative study plans. See Remembered Settings in the Sample Size Explorers.
Reset to Defaults
Resets all parameters and graphs to their default settings.
The Profiler red triangle menu contains the following option:
Optimization and Desirability
Enables you to optimize settings. See “Desirability Profiling and Optimization” in Profilers.
Note: The sample size explorer report can be saved as a *.jmpdoe file. Open the file to return to the explorer. An alert prompts you to save the file.
Statistical Details for the Confidence Interval for Two Independent Sample Means Explorer
Statistical Details for the Confidence Interval for Two Independent Sample Means Explorer
The interval calculations for capturing the difference in population means is based on the standard normal or t distributions based on whether σ1 and σ2 are known or unknown.
The margin of error (MOE) is calculated as follows:
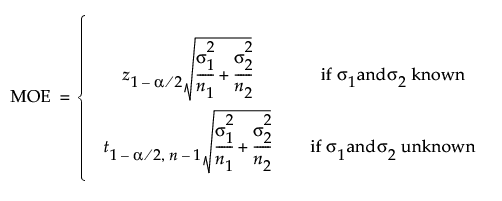
When σ1 and σ2 are unknown, the MOE is calculated as follows:
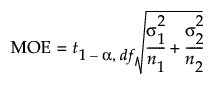
where
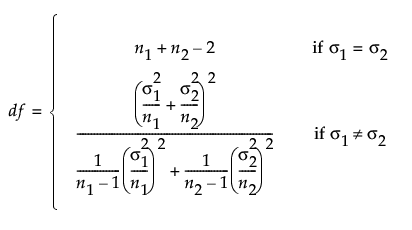
When σ is known, the MOE is calculated as follows:
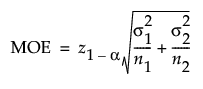
where:
α is the significance level
z1-α is the (1 - α)th quantile of the normal distribution
t1-α,ν is the (1 - α)th quantile of the central t-distribution with ν degrees of freedom
n1 and n2 are the group sample sizes
σ1 and σ2 are the assumed group standard deviations.