 Statistical Details for Causal Estimands and Estimators
Statistical Details for Causal Estimands and Estimators
A causal estimand is a causal effect that one is interested in estimating. An estimator is a function that takes data as input and produces an estimate of the estimand. Different estimators correspond to different methods.
The two causal estimands that can appear in the Causal Treatment report when the treatment is binary are described below. When the treatment is continuous, the Causal Treatment report shows mean potential outcome estimates. See Statistical Details for Continuous Treatment Methods for more information about the continuous treatment scenario.
Average Treatment Effect (ATE)
The average treatment effect (ATE) is the difference in outcomes had the entire population of interest received the treatment X = 1 versus X = 0. The ATE is a causal estimand and is defined as follows:
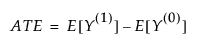
where Y(0) and Y(1) are potential outcomes.
When the treatment is binary, the Causal Treatment personality uses the inverse probability weighted with ratio adjustment (IPWR) estimator, the regression adjusted (REGADJ) estimator, or the augmented inverse probability weighted (AIPW) estimator for the ATE, depending on how the models are specified. These estimates are accurate when the three causal assumptions are met and the ATE is identified from the data.
IPWR Estimator
The IPWR estimator is defined as follows:
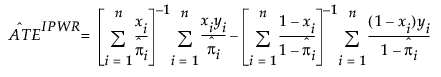
where πi is the probability of receiving treatment X = 1 for observation i (that is, the propensity score) and n is the number of observations in the sample. In the Causal Treatment personality, the propensity score is estimated using the specified treatment model, which is a fitted logistic regression.
REGADJ Estimator
The REGADJ estimator is defined as follows:
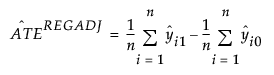
where yi1 and yi0 are the values Y would have taken for observation i had treatment X been set to 1 or 0, respectively, and n is the number of observations in the sample.
In the Causal Treatment personality, yi1 and yi0 are estimated using the specified response model. This model is a fitted logistic regression when the outcome is binary, or a fitted linear regression when the outcome is continuous.
AIPW Estimator
The AIPW estimator is defined as follows:
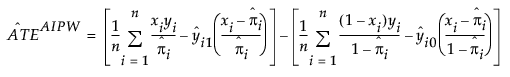
where πi is the propensity score for observation i, yi1 and yi0 are the values Y would have taken for observation i had treatment X been set to 1 or 0, respectively, and n is the number of observations in the sample.
In the Causal Treatment personality, the propensity score is estimated using the specified treatment model, and yi1 and yi0 are estimated using the specified response model.
Average Treatment Effect on the Treated (ATET)
The average treatment effect on the treated (ATET) is the difference in outcomes had the entire population of interest who was treated received the treatment X = 1 versus X = 0. The ATET is a causal estimand and is defined as follows:
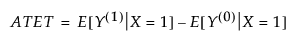
where Y(0) and Y(1) are potential outcomes.
The Causal Treatment personality uses estimators with the same name to estimate the ATET. However, the estimation calculations are different.
IPWR Estimator
The IPWR estimator for the ATET is defined as follows:
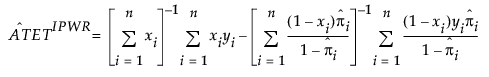
where πi is the propensity score for observation i and n is the number of observations in the sample.
REGADJ Estimator
The REGADJ estimator for the ATET is defined as follows:
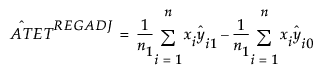
where yi1 and yi0 are the values Y would have taken for observation i had treatment X been set to 1 or 0, respectively, n is the number of observations in the sample, and n1 is the number of observations that received treatment in the sample.
AIPW Estimator
The AIPW estimator for the ATET is defined as follows:
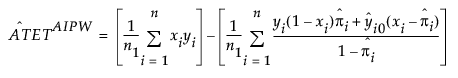
where πi is the propensity score for observation i, yi1 and yi0 are the values Y would have taken for observation i had treatment X been set to 1 or 0, respectively, n is the number of observations in the sample, and n1 is the number of observations that received treatment in the sample.
These estimates are accurate when the three causal assumptions are met and the ATET can be identified from the data.