指定した分布に従う実数を効率的に「サイコロを振る」ことによって生成する計算式を作成できます。計算式エディタで[適用]ボタンをクリックするたびに、これらの関数は新しい乱数を生成します。
メモ: 乱数はMersenne-Twister手法を使って生成されます。この手法の周期は219937-1です。乱数生成の詳細については、Matsumoto and Nishimura(1998)を参照してください。この新しい乱数生成法は、Marshalled(1996)で言及されているすべてのDIEHARDテストに合格しています。
構文の詳細については、『スクリプト構文リファレンス』の「JSL関数」章を参照してください。
0から1までの間で一様乱数を生成します。つまり、0から1までの間のどの実数も、生成される確率は他の実数と同じです。結果は、ほぼ均等な分布になります。定数を使って分布の範囲を変更することもできます。たとえば、5+Random Uniform()*20は、5から25までの間で一様な乱数を生成します。
引数で指定された平均と標準偏差の正規分布に従う乱数を生成します。引数が指定されていない場合は、平均が0で標準偏差が1の正規分布に従う乱数を生成します。正規分布は釣鐘型で左右対称です。平均や標準偏差の引数を指定しなくても、簡単な計算により、特定の平均および標準偏差の正規分布に従う乱数をRandom Normalの結果から生成できます。たとえば、計算式Random Normal()*5+30は、平均が30、標準偏差が5の正規分布に従う乱数を生成します。
たとえば、Random Exp()*0.1はλ=0.1の指数分布を生成します。指数分布は、生存時間や故障時間のデータに使用されることがあります。その場合、λはハザード率(単位時間あたりの故障率)を表します。
形状パラメータalphaのガンマ分布に従う乱数を生成します。ガンマ分布は、あるイベントがK回発生するまでの時間を表します。ガンマ分布には、尺度パラメータbetaを指定することもできます。形状パラメータalphaと尺度パラメータbetaを持ったガンマ分布の乱数は、計算式beta*Random Gamma(alpha)でも生成できます。2*alphaが整数の場合、自由度2*alphaのカイ2乗分布の乱数は、計算式2*Random Gamma(alpha)で生成できます。
位置パラメータが0で尺度パラメータが1のCauchy分布に従う乱数を生成します。Cauchy分布は、釣り鐘型で左右対称ですが、正規分布よりも裾が重い分布です。位置パラメータalphaと尺度パラメータbetaを持ったCauchy変量は、計算式alpha+beta*Random Cauchy()を使って生成することもできます。
指定された確率で発生させたランダムなカテゴリを戻します(たとえば、Random Category(.2, "A", .3, "B", .4, "C", "D");)。
引数で指定されたパラメータを持つ二項分布に従う乱数を生成します。第1引数nは試行回数です。第2引数pは1回あたりの成功する確率です。nが1の場合はBernoulli分布になります。たとえば、n=1およびp=0.5での場合、硬貨を投げたときの分布となります。二項分布の平均はnpで、分散はnp(1 – p)です。
引数で指定されたパラメータを持つ負の二項分布に従う乱数を生成します。第1引数rは成功回数です。第2引数pは1回あたりの成功する確率です。生成される乱数は、r回成功するまでの失敗回数です。試行回数が固定パラメータで成功回数が確率変数の二項分布とは対照的に、負の二項分布は、成功回数が固定パラメータで試行回数が確率変数となります。負の二項分布の平均は(r(1 – p))/pで、分散は(r(1 – p))/p2です。
引数で指定されたパラメータでの幾何分布に従う乱数を生成します。パラメータpは、1回の試行における成功する確率です。幾何分布は、はじめて成功するまでの失敗した試行回数を表すときに使われます。幾何分布の平均は(1-p)/pで、分散は(1 – p)/p2です。
現在のデータテーブルから無作為に行番号を選択します。各行番号は1回だけ選択されます。列に対する添え字にCol Shuffleを指定すると、無作為にその列から値を取得することができます。Col Shuffleの結果、元の列の各値は、1回だけ取得されます。
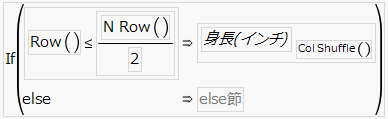
図A.16 50%の標本を無作為に抽出する計算式
50%の標本を無作為に抽出する計算式の計算式は、計算列の最初の半分の行に、x列から無作為抽出した半分の値を割り当てます。計算列の残りの行は欠測値となります。
復元無作為抽出を行った時の度数を戻します。この関数は、ブートストラップ推定を行いたい時に役立ちます。第2引数を指定した場合は、その指定された列を度数列とした復元無作為抽出を行います。引数を何も指定しないで、ResampleFreq()とした場合は、元の標本と同じサイズのデータを抽出します。ResampleFreq(rate)と指定した場合は、行数にrateを掛け合わせたものを標本サイズとします。Resample(rate, column)と指定した場合は、指定した列(column)の合計をrateに掛け合わせたものを度数とします。