推定値の相関
「最小2乗法によるあてはめ」レポートの[推定値の相関]オプションは、パラメータ推定値(パラメータ推定量)の相関行列を計算します。この相関行列は、多重共線性を調べるのに役立ちます。
次のような回帰モデルを考えてみましょう。回帰モデルでは、応答(Y)は、説明変数(x)と誤差(e)の線形関数によって表されます。
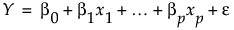
データの各行は、1個の応答変数とp個の説明変数が含まれています。回帰モデルでは、説明変数の値は所与で固定と見なされ、応答変数だけが確率変数と見なされます。
所与の説明変数の値と、確率変数である応答変数の実現値から、パラメータb0、b1、…、bpは推定されます。得られた応答変数の値が変化すれば、パラメータの推定値も変化します。パラメータ推定値はこのような理由で変動します。[推定値の相関]オプションは、パラメータ推定値(パラメータ推定量)の理論上の相関を計算します。技術的な詳細については、カスタム検定の例に関する統計的詳細を参照してください。
パラメータ推定値間の相関は、説明変数の値と切片だけに依存し、応答変数の値には影響されません。2つのパラメータ推定値の間の相関は、応答の値に影響を受けません。
2つの推定値の間に強い相関がある場合、それらの説明変数の間に多重共線性があることが示唆されます。ただし、これらの相関の解釈には注意が必要です(Belsley et al. 1980, p. 185, 92-94)。なお、説明変数から平均を引いて中心化すると、回帰係数の推定値は同じですが、切片パラメータと説明変数に対するパラメータの間の相関は変わります。
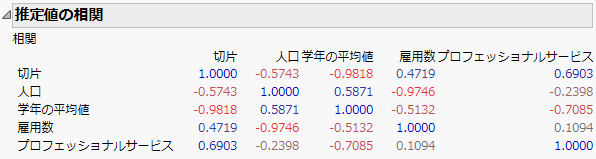
図3.25 「推定値の相関」表
Figure 3.25の「推定値の相関」表を見ると、切片と「学年の平均値」のパラメータ推定値の間に強い負の相関があります(−0.9818)。また、「人口」と「雇用数」のパラメータ推定値の間にも、強い負の相関があります(−0.9746)。