伝達関数モデルの例
この例では、「時系列分析」プラットフォームを使用して伝達関数を特定し、ガス炉の入出力をモデル化する例を紹介します。適切な伝達関数モデルを選択する作業は、反復的な過程です。この例では、入力関数は単位が「立方フィート/分」で測定されたメタンガス供給量です。出力関数は生成されるガス中の二酸化炭素の割合です。この例の詳細については、Box et al.(1994)を参照してください。
「時系列分析」プラットフォームの起動
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Time Series」フォルダにある「seriesJ.jmp」を開きます。
2. [分析]>[発展的なモデル]>[時系列分析]を選択します。
3. 「二酸化炭素 排出量」を選択し、[Y, 時系列]をクリックします。
4. 「入力ガス流量」を選択し、[入力系列リスト]をクリックします。
5. [OK]をクリックします。
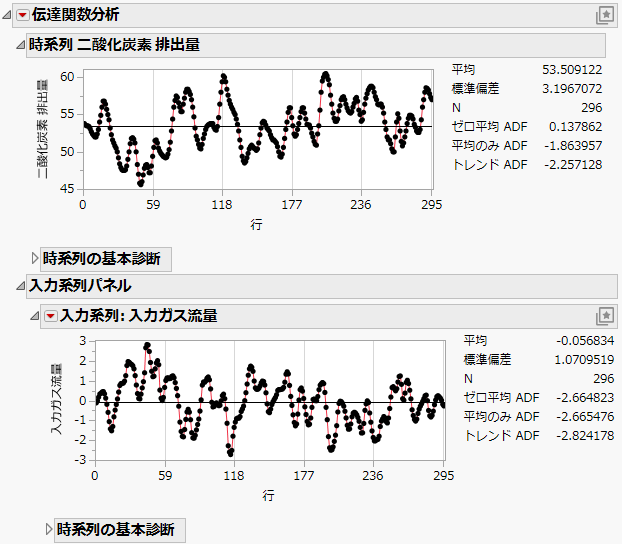
図18.27 最初の「伝達関数分析」レポート
起動ウィンドウで入力変数が指定されたため、「時系列分析」レポートの代わりに「伝達関数分析」レポートが表示されます。この最初のレポートには、出力系列のセクションと入力系列のセクションがあります。各セクションでは、系列と基本的な診断をグラフとして見ることができます。
6. 「入力系列パネル」セクションで、「時系列の基本診断」の横にある三角ボタンをクリックします。
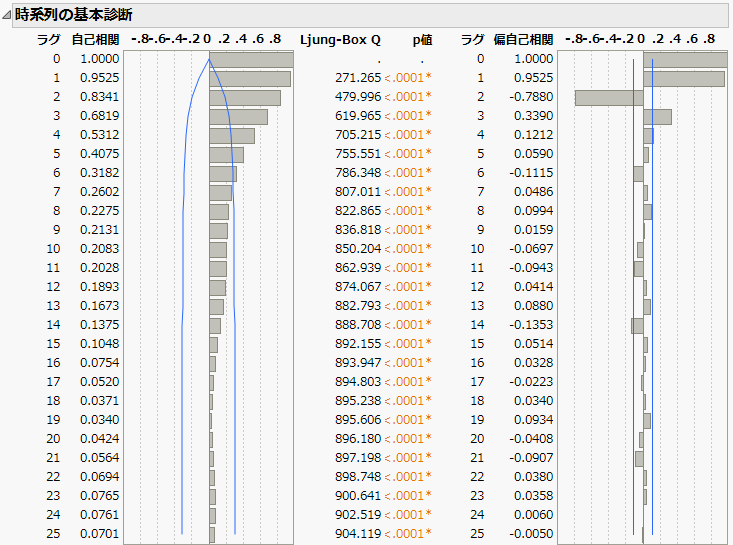
図18.28 「入力ガス流量」の診断
「時系列の基本診断」レポートには、入力系列の自己相関と偏自己相関が表示されます。相関関係に、データに有意な季節傾向を示すような周期的なパターンはありません。したがって、伝達モデルを指定するときに季節パラメータを考慮する必要はありません。
入力データの白色化
伝達関数モデルを特定するのに、まず、白色化(prewhitening)と呼ばれる処理を行います。白色化を行うには、まず、入力系列にうまくあてはまるARIMAモデルを見つけます。入力変数に対する診断を見ることで、どの種類のARIMAモデルを「入力ガス流量」にあてはめるかを決めることができます。「時系列の基本診断」セクションにある偏自己相関プロットを見ると、ラグ3で大きめの偏自己相関を最後に、ラグ4以降では有意な偏自己相関があまりになく、急激に大きさが減少しています。これは、AR(3)モデルが入力系列に適切なARIMAモデルであろうことを示しています。AR(3)モデルで白色化を行う前に、AR(3)モデルをまずあてはめてみて、あてはまりが良いかを個別に確認してみましょう。
1. 「入力系列: 入力ガス流量」の横にある赤い三角ボタンをクリックし、[ARIMA]を選択します。
2. 「ARIMAの指定」ウィンドウで、「p,自己回帰次数」の横に「3」と入力します。
3. [推定]をクリックします。
4. 「残差」が表示されるまで下方向にスクロールし、「残差」の横にある三角ボタンをクリックします。
残差は小さく、明確なパターンはありません。自己相関と偏自己相関も有意ではありません。これらの結果より、AR(3)が白色化で使用するのに適切なARIMAモデルであろうことを確認できました。
5. 「入力系列: 入力ガス流量」の横にある赤い三角ボタンをクリックし、[白色化]を選択します。
6. 「白色化の指定」ウィンドウの「非季節性の次数」セクションで、「p,自己回帰次数」の横に「3」と入力します。
7. [推定]をクリックします。
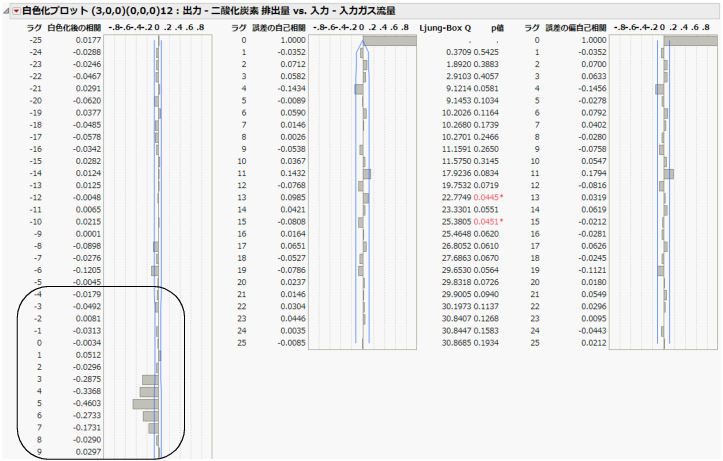
図18.29 「白色化」レポート
この白色化の結果を用いて、伝達関数モデルを特定します。Figure 18.29の四角で囲まれている部分は、この伝達関数モデルの特徴を表す部分です。伝達関数モデルにあまり詳しくない方は、Box et al.(1994)の表を見るといいでしょう。その表に、さまざまな伝達関数モデルに対してインパルス関数がどうなるかが示されています。この表によると、伝達関数モデルのパターンは分子w(B)、分母d(B)ともに次数1または2に対応しているようです。伝達関数モデルの数学的な性質については、伝達関数の統計的詳細を参照してください。その節における記号において、この例では、説明変数の個数は1個だけ(m = 1)なので、w(B)とd(B)の1ペアだけがあります。
最初の有意なゼロでない相互相関はラグ3で生じています。この例の次のステップでは、伝達関数モデルの分子と分母の次数が2、ラグが3であるとして、まずはその予備的な伝達関数モデルをあてはめます。
予備的な伝達関数モデルのあてはめ
1. 「伝達関数分析」の赤い三角ボタンをクリックし、[伝達関数]を選択します。
2. 「伝達関数モデルの指定」ウィンドウで、以下の指定を行います。
– 「s1, 分子演算子の次数」の横に「2」と入力します。
– 「r1, 分母演算子の次数」の横に「2」と入力します。
– 「L, 入力ラグ」の横に「3」と入力します。
– 「予測する期数」の横に「12」と入力します。
3. [推定]をクリックします。
4. 「伝達関数モデル (1)」レポートの「残差」セクションの横にある三角ボタンをクリックします。
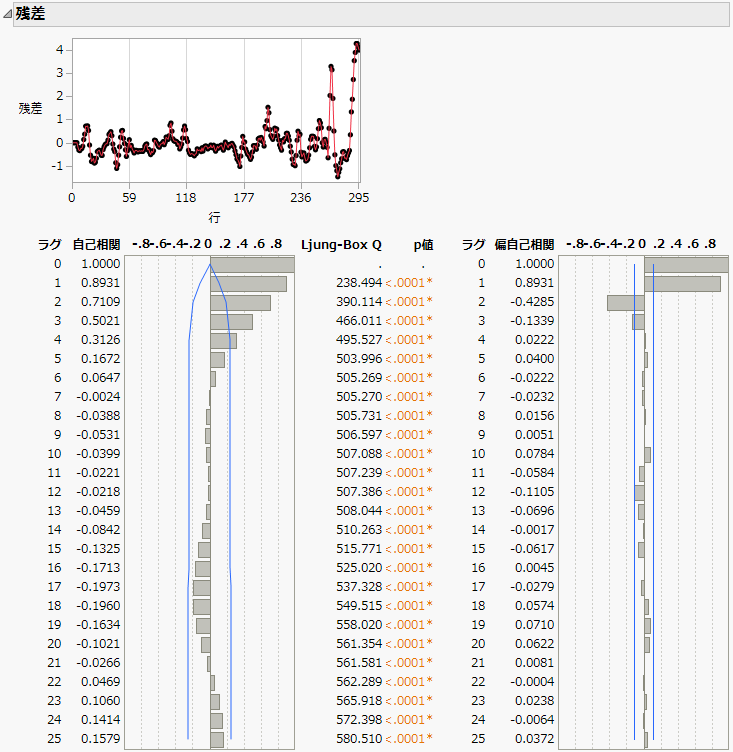
図18.30 予備的な伝達関数モデルの残差
この残差プロットを見ると、観測期間の終わりのほうで残差が大きくなっています。また、有意な自己相関と偏自己相関もあります。これは、予備的な伝達関数モデルが残差間の自己相関に対処していないことを示しています。モデルをデータにより良く適合させるには、モデルのノイズも適切にモデル化する必要があります。偏自己相関を調べると、有意になっている偏自己相関はラグ2までです。これは、ノイズ系列に対してAR(2)モデルがおそらく適切なモデルであろうことを示しています。
5. 「伝達関数分析」の赤い三角ボタンをクリックし、[伝達関数]を選択します。
6. 「伝達関数モデルの指定」ウィンドウで、以下の指定を行います。
– 「p,自己回帰次数」の横に「2」と入力します。
– 「s1, 分子演算子の次数」の横に「2」と入力します。
– 「r1, 分母演算子の次数」の横に「2」と入力します。
– 「L, 入力ラグ」の横に「3」と入力します。
– 「予測する期数」の横に「12」と入力します。
7. [推定]をクリックします。
図18.31 「伝達関数分析」の「モデルの比較」レポート
この「モデルの比較」レポートは、2番目の伝達関数モデルのほうがデータに適合していることを示しています。2番目のモデルは、最初のモデルよりもAICが小さく、R2乗が大きくなっています。
8. 「伝達関数モデル (2)」のレポートまでスクロールします。
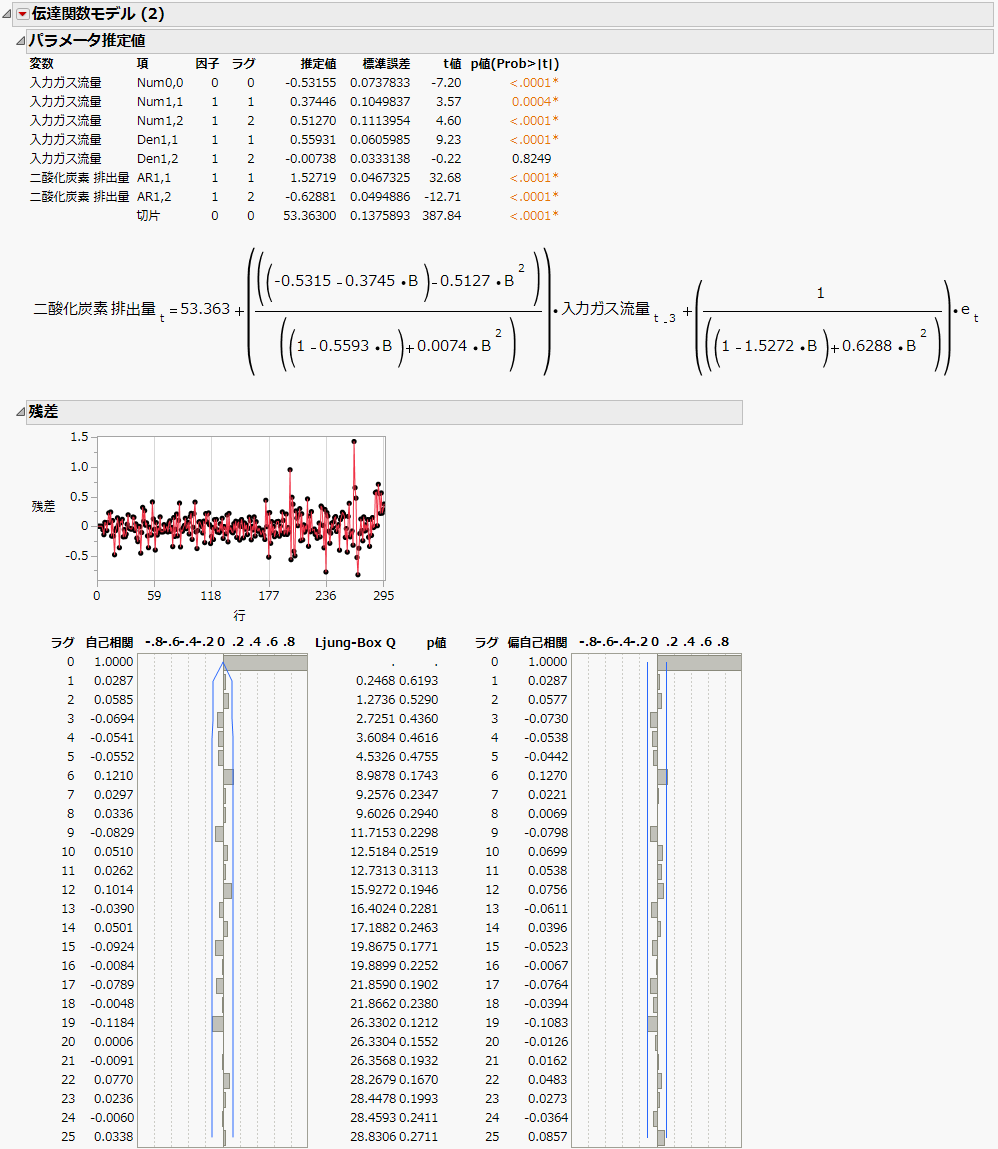
図18.32 最終的な「伝達関数モデル」レポート
残差間には自己相関がなくなっており、この伝達関数モデルが適切なモデルであることがわかります。なお、レポートには、推定されたモデルの式も表示されます。