傾きが等しい共分散分析の例
「モデルのあてはめ」プラットフォームの[標準最小2乗]手法を使って、共分散分析を行います。共分散分析モデルには、興味の対象である主要な因子と、共変量(covariate)の項が1つずつ含まれます。「共変量」とは、主要な因子ではないが、その主要な因子および応答に影響を与えうる変数です。ここで紹介する例では、「薬剤」が主要な因子であり、「x」が共変量です。
メモ: この共分散分析では、主要な因子の各水準において、同じように共変量が応答に影響を与えると仮定します。つまり、傾きが等しい共分散モデルを仮定します。この共分散分析モデルに交互作用項は含まれません。傾きが異なる共分散分析モデルについては、傾きが異なる共分散分析の例を参照してください。
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Drug.jmp」を開きます。
2. [分析]>[モデルのあてはめ]を選択します。
3. 「y」を選択し、[Y]をクリックします。
4. 「薬剤」と「x」の両方を選択し、[追加]をクリックします。
5. [実行]をクリックします。
表示される各レポートの内容を以下に説明していきます。
「回帰プロット」と「予測値と実測値のプロット」
「回帰プロット」や「予測値と実測値のプロット」を見ることで、モデルを評価したり、応答に対する共変量の影響を把握したりできます。
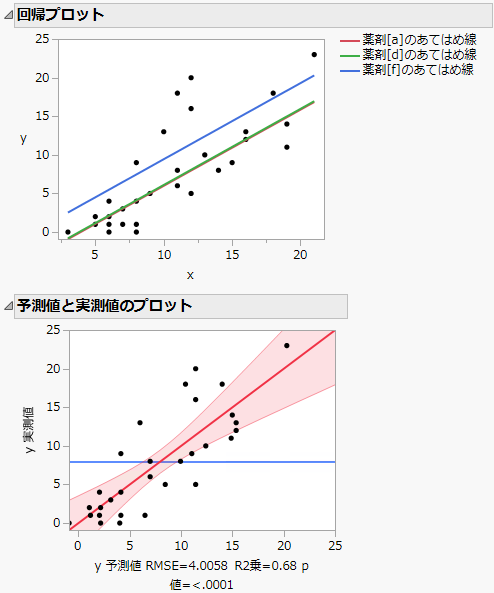
図4.20 傾きが等しい共分散分析のプロット
「回帰プロット」を見ると、回帰直線が平行になっています。これは、モデルとして、傾きが等しいモデルをあてはめたからです。それぞれの薬剤で、応答が共変量「x」に対して同じ割合で増加しています。また、共変量「x」の全水準で、薬剤fの応答が最も大きくなっています。
あてはまりの悪さ(LOF)
このデータは、反復している行があります。たとえば、行1と行9を見てください。両方とも、「薬剤」 = aで「x」= 11になっています。このような反復している行がある場合、それらの行の情報を用いて、純粋誤差(pure erorr)を求めることができます。そして、純粋誤差から、あてはまりの悪さ(LOF; Lack Of Fit)の検定を実行できます。LOF検定が有意な場合、モデルがデータを十分に説明していないことを示唆しています。その場合、共変量の効果が直線的ではなく非線形であったり、交互作用の効果が存在していたりするなどの原因が考えられます。あてはまりの悪さ(LOF)を参照してください。
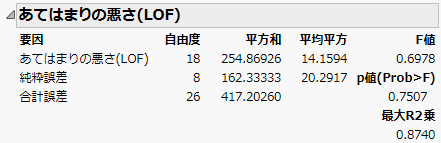
図4.21 傾きが等しい共分散分析のLOF検定
「あてはまりの悪さ(LOF)」レポートの「p値(Prob>F)」の値が0.7507であることから、あてはまりの悪さ(LOF; Lack Of Fit)の検定は有意にはなっていません。
最小2乗平均
最小2乗平均を見て、共変量を考慮に入れた場合の各群の応答の平均値を比較します。
各群の最小2乗平均は、群ごとの単純な標本平均とは異なります。共変量によって値が調整されるためです。各群の最小2乗平均は、共変量xを平均値の10.7333に固定したときの、各群における予測値です。
最小2乗平均は、[パラメータ推定値]レポートで提示されたパラメータ推定値を使って、次のように計算されます。
予測式:
-2.696 - 1.185*薬剤[a] - 1.0761*薬剤[d] + 0.98718*x
a:
-2.696 - 1.185*(1) -1.0761*(0) + 0.98718*(10.7333) = 6.71
d:
-2.696 - 1.185*(0) -1.0761*(1) + 0.98718*(10.7333) = 6.82
f:
-2.696 - 1.185*(-1) -1.0761*(-1) + 0.98718*(10.7333) = 10.16
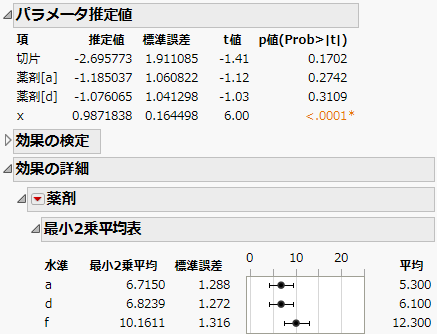
図4.22 薬剤実験データの「パラメータ推定値」と「最小2乗平均表」