傾きが異なる共分散分析の例
「モデルのあてはめ」プラットフォームの[標準最小2乗]手法を使って、共分散分析を行います。共分散分析モデルには、興味の対象である主要な因子と、共変量(covariate)の項が1つずつ含まれます。「共変量」とは、主要な因子ではないが、その主要な因子および応答に影響を与えうる変数です。ここで紹介する例では、「薬剤」が主要な因子であり、「x」が共変量です。
メモ: この分析では、主要な因子の各水準において、共変量が応答に異なる影響を与えていると仮定します。つまり、傾きが異なる共分散分析モデルを仮定します。この共分散分析モデルには交互作用項が含まれます。傾きが等しいモデルについては、傾きが等しい共分散分析の例を参照してください。
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Drug.jmp」を開きます。
2. [分析]>[モデルのあてはめ]を選択します。
3. 「y」を選択し、[Y]をクリックします。
4. 「薬剤」と「x」の両方を選択し、[マクロ]>[設定された次数まで]をクリックします。
これにより、「次数」ボックスで指定した次数までの項がモデルに追加されます。「次数」のデフォルト値は2です。これで、「薬剤」と「x」の主効果と、それらの交互作用である「薬剤*x」がモデル効果のリストに追加されたはずです。
5. [実行]をクリックします。
「薬剤」および「薬剤」と「x」の交互作用に使用したコード変換をTable 4.1に示します。
|
説明変数 |
効果 |
値 |
|
x1 |
薬剤[a] |
aのとき+1、dのとき0、fのとき–1 |
|
x2 |
薬剤[d] |
aのとき0、dのとき+1、fのとき–1 |
|
x3 |
X |
xの値 |
|
x4 |
薬剤[a]*(x – 10.733) |
aのときx – 10.7333、dのとき0、fのとき–(x – 10.7333) |
|
x5 |
薬剤[d]*(x – 10.733) |
aのとき0、dのときx – 10.7333、fのとき–(x – 10.7333) |
表示される各レポートの内容を以下に説明していきます。
「回帰プロット」と「効果の検定」
「回帰プロット」を見ることで、モデルを評価したり、共変量が応答に与える影響を把握したりできます。また、「効果の検定」では、効果の統計的有意性を求めることができます。
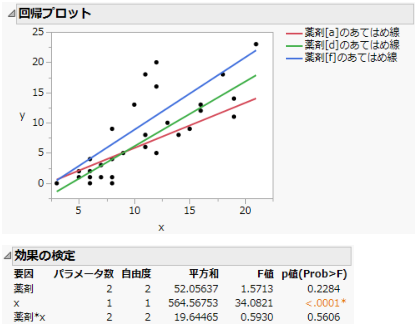
図4.23 「回帰プロット」と「効果の検定」(交互作用がある場合)
「回帰プロット」では、薬剤dとfにおいては、共変量「x」に対してほぼ同じ割合で応答が増加していることが示されています。薬剤aにおいては、これらの2つの薬剤に比べ、応答の増加の割合が小さくなっています。一方、「効果の検定」を見ると、交互作用のp値は0.56で、統計的には有意でありません。
スポットライト分析の実行
次に、共変量xの特定の値で「薬剤」の水準の最小2乗平均を比較します。共分散分析モデルなどにおけるこのような比較は、「スポットライト分析」と呼ばれることがあります。スポットライト分析の詳細については、Spiller et al.(2013)を参照してください。
1. 「応答 y」の赤い三角ボタンのメニューから、[多重比較]を選択します。
2. 「多重比較」ウィンドウで、[ユーザ定義の推定値]を選択します。
3. [薬剤の水準を選択]の下の3つの値をすべて選択します。
4. xの下の最初のボックスに「12.5」と入力します。
5. [推定値の追加]をクリックします。
これは、3水準の[薬剤]をx = 12.5で比較したものを追加します。
6. [OK]をクリックします。
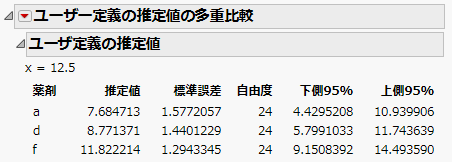
「ユーザ定義の推定値」レポートには、共変量xを12.5に設定した[薬剤]の各レベルの最小2乗平均の推定が表示されます。「ユーザ定義の推定値の多重比較」の赤い三角ボタンのメニューには、推定値の間の差を検定するオプションが含まれています。
図4.24 「ユーザ定義の推定値」レポート
7. 「ユーザ定義の推定値の多重比較」の赤い三角ボタンのメニューから、[全体平均との比較]を選択します。
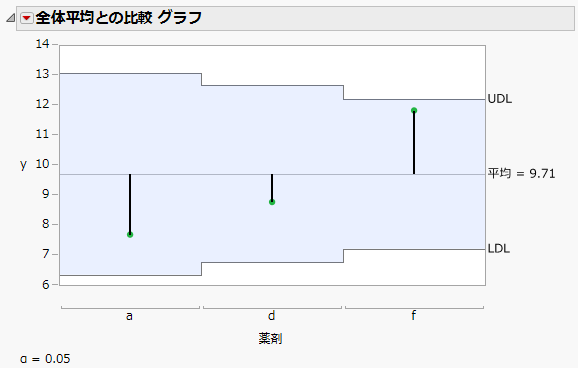
図4.25 全体平均との比較 グラフ
[全体平均との比較]オプションは、平均と3つの最小2乗平均との間の差に対する平均分析(ANOM; analysis of means)を表示します。平均分析(ANOM)のグラフにおいて、x = 12.5での全体平均からの差を見る限り、[薬剤]の統計的に有意な効果はありません。