[一般化線形混合モデル]手法の起動
[一般化線形混合モデル]手法の起動
[一般化線形混合モデル]手法を起動するには、[分析]>[モデルのあてはめ]を選択します。1つ以上の列を[Y]に指定し、「手法」メニューから[一般化線形混合モデル]を選択します。
 「モデルのあてはめ」起動ウィンドウ
「モデルのあてはめ」起動ウィンドウ
モデル効果として、固定効果と変量効果のいずれかまたは両方を指定できます。応答変数の分布も指定できます。起動ウィンドウに表示されるオプションは、指定したモデルの種類によって異なります。「列の選択」の赤い三角ボタンのメニューのオプションについては、『JMPの使用法』の“Column Filter Menu”を参照してください。
[一般化線形混合モデル]を使ってモデルをあてはめる場合、[分散成分の範囲制限なし]というオプションが表示されます。このオプションがオンになっている場合、分散の推定値が負になることを許容します。このオプションは、デフォルトでオンになっています。固定効果に対する検定に主に興味がある場合は、このオプションをオンにしておいたほうが良いでしょう。分散推定値に非負の制約を課すと、固定効果の検定にバイアス(偏り)が生じるためです。[分散成分の範囲制限なし]の詳細は、負の分散推定値を参照してください。
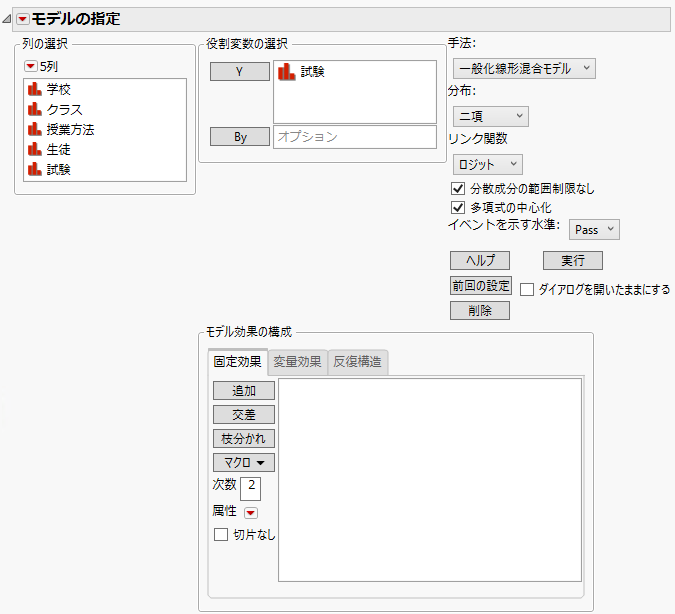
図9.6 [一般化線形混合モデル]手法を選択した「モデルのあてはめ」起動ウィンドウ
すべての手法に共通の「モデルのあてはめ」ウィンドウの要素の詳細については、モデルの指定を参照してください。「列の選択」の赤い三角ボタンのメニューのオプションについては、『JMPの使用法』の“Column Filter Menu”を参照してください。ここでは、[一般化線形混合モデル]手法に固有の情報を紹介します。
 分布の指定
分布の指定
「モデルのあてはめ」起動ウィンドウで[一般化線形混合モデル]手法を選択すると、「分布」オプションが表示されます。ここで、Yの分布を指定できます。選択可能な分布の種類について、以下で説明します。
正規
応答Yが、平均m、標準偏差sの正規分布に従っていると仮定されます。正規分布は対称な分布です。さまざまな分布において、標本サイズが大きい場合、その標本平均は正規分布に従います(中心極限定理)。mに対するリンク関数は恒等関数です。つまり、Yの平均が、線形モデルに等しいと仮定されます。
指数
応答Yが、平均パラメータmの指数分布に従っていると仮定されます。指数分布は右に裾をひいた形状です。生存時間や連続するイベント間の時間をモデル化するのによく使用されます。mに対するリンク関数は、対数です。
ガンマ
応答Yが、平均パラメータmとばらつきパラメータsのガンマ分布に従っていると仮定されます。ガンマ分布には柔軟性があり、他のいくつかの分布と関係しています。たとえば、指数分布は、s = mの場合のガンマ分布です。また、カイ2乗分布もガンマ分布に属します。mに対するリンク関数は、対数です。
対数正規
応答Yが、位置パラメータmと尺度パラメータsの対数正規分布に従っていると仮定されます。対数正規分布は右に裾をひいた形状です。生存時間や連続するイベントが発生するまでの時間をモデル化するのによく使用されます。mに対するリンク関数は、恒等関数です。
ベータ
応答Yが、平均パラメータm、ばらつきパラメータsのベータ分布に従っていると仮定されます。ベータ分布の応答は、0より大きく1より小さい値で、割合や比率を表すのによく使用されます。mに対するリンク関数は、ロジット関数です。
二項
応答Yが、パラメータがnとpの二項分布に従っていると仮定します。二項分布における応答Yは、n回の独立した試行を行ったときの成功回数です。各試行内においては、成功確率pは一定です。二項分布では、成功回数だけではなく、試行回数も与える必要があります。手法の[二項]分布では、試行回数を含む列を明示的に指定しなかった場合には、試行回数は1とみなされます。手法で[二項]分布を選択した場合、pに対するリンク関数には、デフォルトでロジット関数が使われます。「モデルのあてはめ」起動ウィンドウの「リンク関数」オプションで、[プロビット]に変更することもできます。応答変数として2値の名義尺度の列を選択した場合、使用できる分布は[二項]分布だけに限られます。
[二項]分布を選択した場合は、応答変数のデータが次のいずれかの形式になっていなければいけません。
– データが要約されていない場合: データが要約されていない場合は、2値データを含んでいる列1つを、応答として指定します。この列が名義尺度の場合は、水準の1つを「イベントを示す水準」に指定できます。2水準のうち、順序が後のほうの値が、「イベントを示す水準」のデフォルト値です。
– データが要約されていて、度数が2列に含まれている場合: データが要約されていて、成功回数と試行回数の2列がある場合は、「Y」に対して、成功回数を含む列、次に試行回数を含む列の順に指定します。この場合、2列とも連続尺度でなければいけません。
Poisson
応答Yが、平均lのPoisson分布に従っていると仮定します。Poisson分布は、一定期間内に生じているイベントの回数などの度数データに対して、よく使われます。手法で[Poisson]分布を選択した場合、パラメータlに対するリンク関数には、対数が使われます。なお、応答Yに整数以外の数値がある場合でも実行できます。
負の二項
応答Yが、平均m、過分散パラメータsの負の二項分布に従っていると仮定されます。負の二項分布は通常、特定の失敗回数に達するまでの成功回数をモデル化するのに使われています。また、負の二項分布はガンマPoisson分布を別のパラメータ表現したものです。負の二項分布とガンマPoisson分布との関係の詳細については、『基本的な統計分析』の“Distributions”を参照してください。
JMPの「Samples」フォルダ内の「Scripts」フォルダにある「demoGammaPoisson.jsl」を実行すると、平均lのPoisson分布と、平均lおよび過分散パラメータsのガンマPoisson分布とを比較できます。
mに対するリンク関数は、対数です。なお、応答Yに整数以外の数値がある場合でも実行できます。
次の表に、それぞれの分布について、応答Yに指定できる列のデータタイプと尺度を示します。
分布 | データタイプ | 尺度 | その他 |
|---|---|---|---|
正規 | 数値 | 連続尺度 |
|
指数 | 数値 | 連続尺度 | 0以上の数値 |
ガンマ | 数値 | 連続尺度 | 正の数値 |
対数正規 | 数値 | 連続尺度 | 正の数値 |
ベータ | 数値 | 連続尺度 | 0~1 |
二項(要約していないもの) | すべて | すべて | 二値 |
二項(2列の度数に要約) | 数値 | 連続尺度 | 0以上の数値 |
Poisson | 数値 | すべて | 0以上の数値 |
負の二項 | 数値 | すべて | 0以上の数値 |
次の表に、分布のパラメータおよびリンク関数の一覧を示します。
分布 | パラメータ | リンク関数 |
|---|---|---|
正規 | m, s | 恒等(m) |
指数 | m | Log(m) |
ガンマ | m, s | Log(m) |
対数正規 | m, s | 恒等(m) |
ベータ | m | Logit(m) |
二項 | n, p | Logit(p) Probit(p) |
Poisson | l | Log(m) |
負の二項 | m, s | Log(m) |
 [固定効果]タブ
[固定効果]タブ
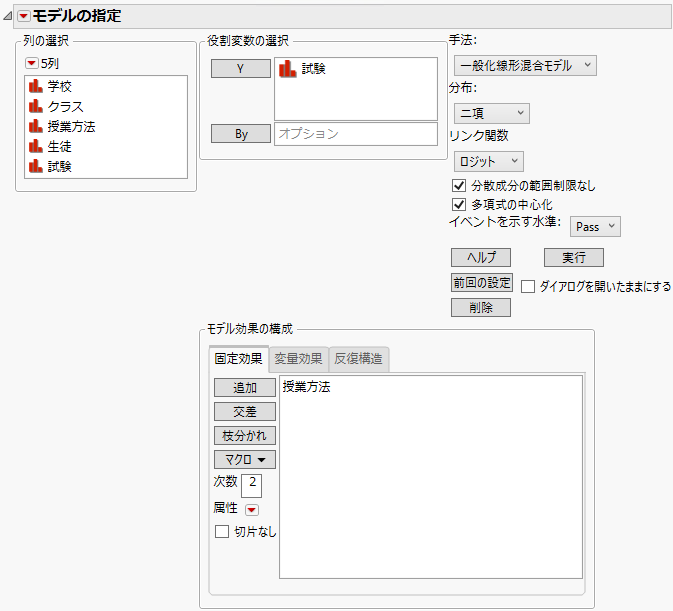
[固定効果]タブにすべての固定効果を追加します。必要に応じて、[追加]・[交差]・[枝分かれ]・[マクロ]・[属性]の各オプションを使用します。これらのオプションの詳細については、モデルの指定を参照してください。なお、データやモデルによっては1つも固定効果がないものもありえます。
メモ: 「モデルの指定」の赤い三角ボタンのメニューから[多項式の中心化]を選択した場合でも、変量効果に含まれている連続尺度の列は中心化されません。
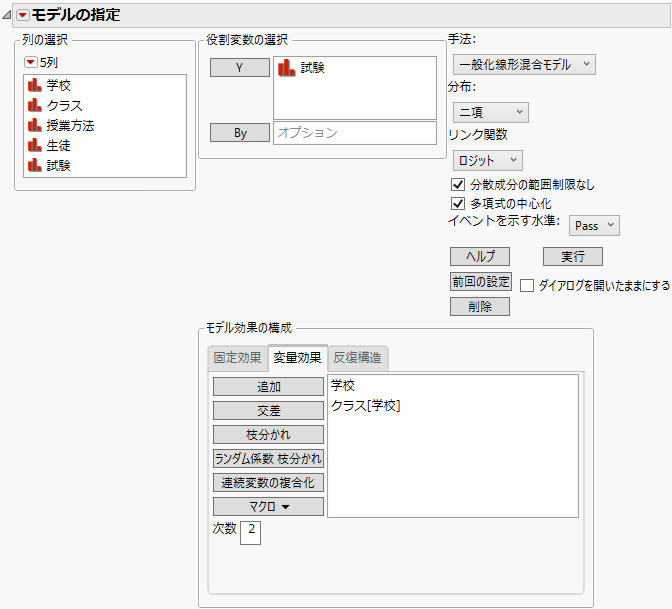
図9.7 指定が完了した「モデルのあてはめ」起動ウィンドウの[変量効果]タブ
 [変量効果]タブ
[変量効果]タブ
[変量効果]タブは、従来の分散成分モデルや、ランダム係数モデルを指定するときに用います。
メモ: 「モデルの指定」の赤い三角ボタンのメニューから[多項式の中心化]を選択した場合でも、変量効果に含まれている連続尺度の列は中心化されません。
分散成分モデル
従来の分散成分モデルを指定する場合は、[追加]・[交差]・[枝分かれ]オプションを使用して、乱塊実験におけるブロック効果や、分割実験における1次単位効果などの変量効果を指定します。これらのオプションの詳細については、モデルの指定を参照してください。
図9.8 [変量効果]を指定した「モデルのあてはめ」起動ウィンドウ
ランダム係数
ランダム係数モデルを作成するには、[ランダム係数 枝分かれ]ボタンを使ってランダム係数のグループを作成します。
1. 「列の選択」リストから、説明変数となる連続尺度の列を選択します。
2. [変量効果]タブを選択し、[追加]をクリックします。
3. [変量効果]タブで連続尺度の説明変数の列を選択して(説明変数が複数ある場合には、それらすべてを選択してください)、さらに、「列の選択」リストにおいて個々の回帰モデルに該当する水準の列を選択します。
4. [ランダム係数 枝分かれ]ボタンをクリックします。
この最後の操作により、ランダムな切片とランダムな(複数の)傾きがモデルに追加されます。なお、切片と(複数の)傾きの間には、すべて相関が仮定されます。この最後の操作では、ランダムな切片も自動的に追加される点に注意してください。「切片はすべてのグループで共通で固定されている」と仮定するなら、「切片[<グループ>]& ランダム係数(1)」を選択して[削除]をクリックすると、ランダムな切片がモデルから削除されます。
同様の手順を繰り返すことにより、ランダム係数に関して複数のグループを指定できます。これにより、より複雑なランダム係数モデルを指定できます。たとえば、製造業の分割実験において、バッチの効果と、処置とバッチの交互作用という、2つの効果を含めたランダム係数モデルを指定できます。また、教育効果の調査においては、学校の効果と、(学校から枝分かれした)生徒の効果という、2つの効果を含めたランダム係数モデルを指定できます。
 [反復構造]タブ
[反復構造]タブ
[反復構造]タブは、誤差の共分散構造を選択するのに使用します。
表9.3 「モデルのあてはめ」起動ウィンドウの[反復構造]タブでの指定
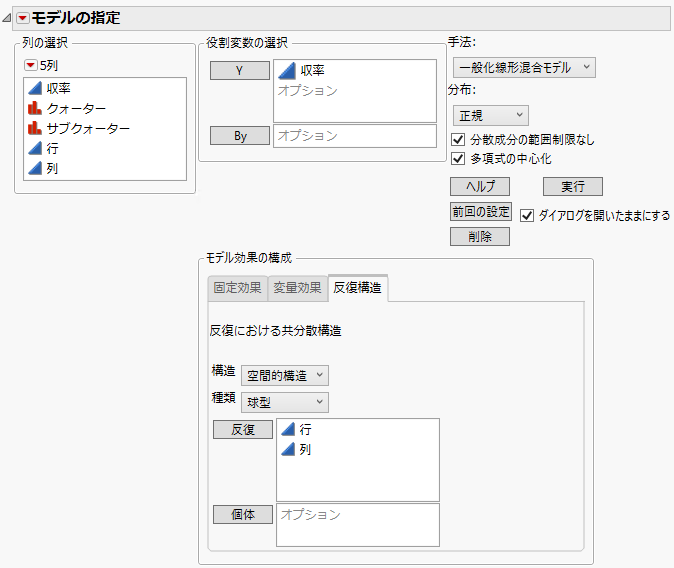
構造
反復構造は、デフォルトでは[なし]に設定されています。反復構造として[なし]を指定した場合、「誤差間には共分散が存在しない」、つまり、「誤差は互いに独立している」と仮定されます。その他のすべての共分散構造は、誤差間に何らかの共分散があると仮定されます。
Table 9.4に、使用できる共分散構造と、各構造を使用するための要件、各構造の共分散パラメータの数をリストします。観察時点数はJとします。
構造 | 反復列の種類 | 反復列の必要数 | 個体の指定 | パラメータ数 |
|---|---|---|---|---|
なし |
| 0 |
| 0 |
無構造 | カテゴリカル | 1 | 必須 | J(J+1)/2 |
AR(1) | 連続尺度 | 1 | オプション | 2 |
複合対称 | カテゴリカル | 1 | 必須 | 2 |
Toeplitz | カテゴリカル | 1 | 必須 | J |
先行依存 | カテゴリカル |
| 必須 | 2J-1 |
空間的構造 | 連続尺度 | 2+ | オプション |
|
共分散構造として[なし]を指定した場合、[反復]や[個体]の列に指定された列は無視されます。「共分散構造として「残差」が選択されているので、[反復]や[個体]に指定された列を無視して分析を行います。」という警告が表示されます。
種類
共分散構造として[空間的構造]を指定した場合、「種類」リストが表示されます。このリストから空間的構造を表す関数を1つ選択します。[べき乗]・[指数]・[Gauss]・[球型]という4種類があります。
反復
反復測定構造を定義する列を入力します。この[反復]に指定できる列の尺度は、共分散構造によって異なります。反復測定の共分散構造ごとの要件について、Table 9.4を参照してください。
要素
個体を定義する1つまたは複数の列を入力します。個体の列は、カテゴリカルでなければなりません。
 データ形式
データ形式
「モデルのあてはめ」プラットフォームの[一般化線形混合モデル]手法では、すべての応答変数の測定値は1列に含まれている必要があります。反復測定データは、複数の列に保存されていることもあるでしょう。つまり、それぞれの行が1個体を表しており、各時点での測定値が別々の列に記録されていることがあるでしょう。データがそのような形式である場合は、データを積み重ねてから[一般化線形混合モデル]手法を実行する必要があります。「Cholesterol.jmp」および「Cholesterol Stacked.jmp」サンプルデータテーブルは、それぞれ応答値を複数列に保存している形式と積み重ねた形式になっています。複数列に保存している形式におけるデータの各行は、積み重ねた形式のデータにおける「患者」1人に対応しています。