溶出曲線分析の統計的詳細
この節では、「曲線のあてはめ」プラットフォームのモデルフリー溶出曲線分析で算出される指標(F1・F2・多変量距離)について説明します。次のような記号を用います。
mRiを、時点tiにおける標準薬剤群の溶出値の平均とします。
mTiを、時点tiにおける試験製剤群の溶出値の平均とします。
i = 1, ..., Nを、観測時点に対する通し番号とします。
F1(溶出曲線の違いを示す指標)
F1は、標準製剤の溶出曲線と試験製剤の溶出曲線との間に見られる違いをパーセントで表したものです。F1は以下の式を使って計算されます。
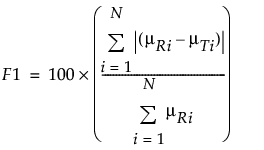
F2(溶出曲線の類似性を示す指標)
F2は、標準製剤の溶出曲線と試験製剤の溶出曲線との間に見られる類似性をパーセントで表したものです。F2は以下の式を使って計算されます(Paixão et al. 2017)。
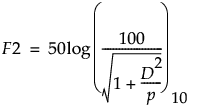
ここで
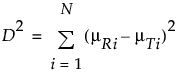
pは、観測時点の数
Mahalanobisの距離
Mahalanobis距離Mは、標準製剤の溶出曲線と試験製剤の溶出曲線との間の多変量距離です。Mは以下の式を使って計算されます(Paixão et al. 2017)。
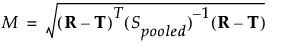
ここで
R = [mR1,...,mRN]T
T = [mT1,...,mTN]T
Spooled = (SR + ST)/2
SR = 標準製剤における曲線値の共分散行列
ST = 試験製剤における曲線値の共分散行列
10%差距離は、次の式を使用して計算されます。
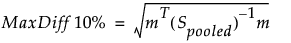
ここで、mは10のNx1ベクトルです。
T2EQ
WellekのT2手法の検定統計量T2は、Mahalanobisの距離で計算されるMahalanobisの距離Mを使用します。
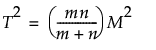
ここで
m = 標準製剤の曲線の本数
n = 試験製剤の曲線の本数
M = Mahalanobisの距離
この検定統計量は、非心F分布に従います。検定統計量のp値は、次の式を使用して計算されます(Hoffelder 2019):
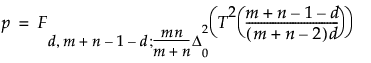
ここで
Fs1, s2; nc(x)は非心F分布の累積分布関数です。
d = 治験における観測時点の数
D20 = 差の幅
JMPでの計算では、上記の「差の幅」として10を使用しています。