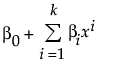「曲線のあてはめ」モデルの統計的詳細
Table 14.1に、「曲線のあてはめ」の赤い三角ボタンのメニューで用意されているモデルの計算式を示します。
|
モデル |
計算式 |
|---|---|
|
多項式
|
kは多項式の次数です。これらのモデルは、「モデルのあてはめ」プラットフォームや「二変量の関係」プラットフォームでもあてはめることができます。 |
|
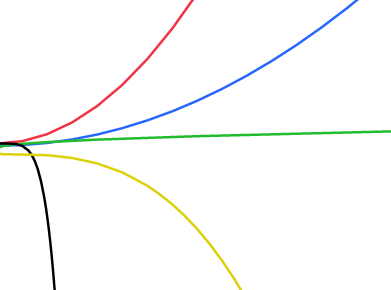
べき乗モデル
|
a = 切片 b = 傾き c = べき乗 応答変数とxの値が負でない場合にのみ使用可能です。 |
|
ロジスティック 2P
|
a = 増加率 b = 変曲点 応答変数のすべての値が0~1である場合にのみ使用可能です。 |
|
ロジスティック 3P
|
a = 増加率 b = 変曲点 c = 漸近線 |
|
ロジスティック 4P
|
a = 増加率 b = 変曲点 c = 下側漸近線 d = 上側漸近線 |
|
ロジスティック 4P Rodbard
|
a = 増加率 b = 位置 c = 下側漸近線 d = 上側漸近線 xの値が正の場合にのみ使用可能です。 |
|
ロジスティック 4P Hill
|
a = 増加率 b = 変曲点 c = 下側漸近線 d = 上側漸近線 |
|
ロジスティック 5P
|
a = 増加率 b = 位置 c = 漸近線1 d = 漸近線2 f = べき乗 |
|
プロビット 2P
|
a = 増加率 b = 変曲点 F = 正規分布累積確率 応答変数のすべての値が0~1である場合にのみ使用可能です。 |
|
プロビット3P
|
a = 増加率 b = 変曲点 c = 漸近線 F = 正規分布累積確率 ゼロの位置には漸近線もあります。 |
|
プロビット 4P
|
a = 増加率 b = 変曲点 c = 下側漸近線 d = 上側漸近線 F = 正規分布累積確率 |
|
Gompertz 3P
|
a = 漸近線 b = 増加率 c = 変曲点 |
|
Gompertz 4P
|
a = 下側漸近線 b = 上側漸近線 c = 増加率 d = 変曲点 |
|
Weibull成長
|
a = 上方漸近線 b = 位置 c = 増加率 応答変数とxの値が負でない場合にのみ使用可能です。 |
|
指数 2P
|
a = スケール b = 増加率 |
|
指数 3P
|
a = 漸近線 b = スケール c = 増加率 |
|
双指数 4P
|
a = スケール1 b = 減衰率1 c = スケール2 d = 減衰率2 応答変数の値が正の場合にのみ使用可能です。 |
|
双指数 5P
|
a = 漸近線 b = スケール1 c = 減衰率1 d = スケール2 f = 減衰率2 |
|
単分子成長
|
a = 漸近線 b = スケール c = 増加率 |
|
ハイブリッド指数
|
a = 最大値 b = スケール c = 比率 d = べき乗 応答変数とxの値が負でない場合にのみ使用可能です。 |
|
細胞成長 4P
|
a = 死亡率dがゼロの場合のピーク値 b = 時間ゼロにおける応答 c = 細胞分裂率 d = 細胞死亡率 応答変数の値が正で、かつxの値が負でない場合にのみ使用可能です。 |
|
Gauss型ピーク
|
a = ピーク値 b = 臨界点 c = 増加率 |
|
非対称Gaussピーク
|
a = 最適解 b = スケール1 c = スケール2 d = ピーク値 応答変数の値が0以上の数値の場合にのみ使用可能です。 |
|
歪正規 ピーク
|
a = 位置 b = スケール c = 歪み具合 d = ピーク値 f = 標準正規分布の確率密度関数 応答変数の値が0以上の数値の場合にのみ使用可能です。 |
|
ExGaussian型ピーク
|
a = AUC(曲線の下の面積) b = 位置 c = スケール d = Lambda f = 標準正規分布の確率密度関数 |
|
擬似Voigtピーク
|
d = 混合パラメータ l(x) = Lorentz型ピーク関数 l(x) = Gauss型ピーク関数 応答変数の値が0以上の数値の場合にのみ使用可能です。 |
|
Pearson VII ピーク
|
a = 位置 b = スケール c = 形状 d = ピーク値 応答変数の値が0以上の数値の場合にのみ使用可能です。 |
|
Lorentz型ピーク
|
a = ピーク値 b = 増加率 c = 臨界点 |
|
1コンパートメント 経口投与
|
a = AUC(曲線下面積) b = 消失速度 c = 吸収速度 応答変数の値とxの値がすべて正の場合にのみ使用可能です。 |
|
2コンパートメント 急速静注
|
a = b = a = 初期濃度 b = 移行速度 流入 c = 移行速度 流出 d = 消失速度 応答変数の値とxの値がすべて正の場合にのみ使用可能です。 |
|
Michaelis-Menten
|
a = 最大速度 b = Michaelis定数 応答変数の値とxの値がすべて正の場合にのみ使用可能です。 |
|
逆Inverse Michaelis-Menten
|
a = 最大速度 b = Michaelis定数 応答変数の値とxの値がすべて正の場合にのみ使用可能です。 |
|
1次速度
|
a = 初期値 b = 速度定数 xの値が負でない場合にのみ使用可能です。 |
|
可逆1次速度
|
a = 初期値 b = 下限値 c = 速度定数 xの値が負でない場合にのみ使用可能です。 |
|
可逆1次速度
|
a = 初期値 b = 正反応速度 c = 逆反応速度 xの値が負でない場合にのみ使用可能です。 |
|
2次反応速度
|
a = 初期値 b = 速度定数 xの値が負でない場合にのみ使用可能です。 |
|
2コンポーネント2次速度
|
a = 初期値 b = オフセット c = 速度定数 xの値がいずれも負でない場合にのみ使用可能です。 |
|
Antoine
|
a = 成分固有の定数 b = 成分固有の定数 c = 成分固有の定数 応答変数の0より大きい場合にのみ使用可能です。 垂直の漸近線は10aの位置にあります。 水平の漸近線は−cの位置にあります。 |
|
Higuchi
|
a = 放出定数 xとyのすべての値が負でない場合にのみ使用可能です。 |
|
ラグを含むHiguchi
|
a = 放出定数 b = タイムラグ xとyのすべての値が負でない場合にのみ使用可能です。 |
|
バーストを含むHiguchi
|
a = 放出定数 b = バースト xとyのすべての値が負でない場合にのみ使用可能です。 |
|
Hixson-Crowell
|
a = 放出定数 xとyのすべての値が負でない場合にのみ使用可能です。 |
|
ラグを含むHixson-Crowell
|
a = 放出定数 xとyのすべての値が負でない場合にのみ使用可能です。 |
|
Korsmeyer-Peppas
|
a = 放出定数 b = 拡散指数 xとyのすべての値が負でない場合にのみ使用可能です。 |
|
ラグを含むKorsmeyer-Peppas
|
a = 放出定数 b = 拡散指数 c = タイムラグ xとyのすべての値が負でない場合にのみ使用可能です。 |
|
バーストを含むKorsmeyer-Peppas
|
a = 放出定数 b = 拡散指数 c = バースト xとyのすべての値が負でない場合にのみ使用可能です。 |