媒介分析の統計的詳細

ここでは、結果変数（y）と媒介変数（M）の媒介分析で使用される連立一次方程式について、最も簡単な例とともに説明します。原因変数（x）と媒介変数（M）および原因変数（x）と結果変数（y）の間の関係を、次のように表します。

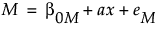
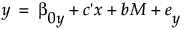
最初の式は、媒介変数（M）に対する原因変数（x）の効果を示しています。原因変数（x）が1単位増加するごとに、媒介変数（M）はa単位増加すると予想されます。2番目の式は、媒介変数（M）の値がまったく同じ2つの個体がある場合、原因変数（x）の値が大きい方が、結果変数（y）に対してc'単位の変化をもたらすことを示します。直接効果（c'）が正の値を示す場合、媒介変数が同じ値ならば、原因変数（x）が増加すると、結果変数（y）も増加する可能性が高いです。一方、効果が負の値を示す場合、媒介変数が同じ値ならば、原因変数（x）が増加すると、結果変数（y）は減少する可能性が高いです。

これらの式をもとに、この媒介分析モデルにおける直接効果と間接効果を定義できます。これらの式は、次のように変形できます。

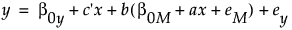
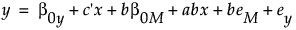
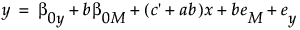
変形した式から、以下のことが言えます。

b0y + bb0Mは、新しい切片です。

c' + abは、新しい傾きです。この新しい傾きは、総合効果（c）と呼ばれ、直接効果（c'）と間接効果（ab）で構成されます。

beM + eyは、新しい誤差項です。

総合効果は次のように定義することができます。

総合効果（c）= 直接効果（c' ）+間接効果（ab）

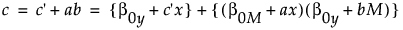
より詳細な情報が必要な場合や、質問があるときは、JMPユーザーコミュニティで答えを見つけましょう (community.jmp.com).