「あてはめの要約」指標の統計的詳細
この節では、「構造方程式モデル」プラットフォームの「あてはめの要約」に示される統計量について説明します。
AICc・BIC・BICu
AICcとBICは次のように定義されます。
AICc = 
BIC =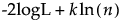 
ここで
-2logLは、対数尤度をマイナス2倍したもの。
nは、標本サイズ。
kは、パラメータの個数。
「モデルの比較」レポートに表示される尤度に基づく指標については、『基本的な回帰モデル』の「Likelihood, AICc, and BIC」を参照してください。
「飽和モデルに対するBIC」（BICu; BIC relative to the unrestricted model）は次のように定義されます。
BICu = 
ここで
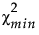は、あてはめたモデルに対するカイ2乗。
dfminは、あてはめたモデルに対するカイ2乗の自由度。
nは、標本サイズ。
現モデルのBICuは、現モデルのBICから飽和モデルのBICを引いたものに相当します。飽和モデルに対するBICの詳細については、Bollen et al.（2014）を参照してください。
CFI
比較適合度指標（CFI; Comparative Fit Index）は次のように定義されます。
CFI = 
ここで
は、独立モデルに対するカイ2乗。
df0は、独立モデルに対するカイ2乗の自由度。
は、あてはめたモデルに対するカイ2乗。
dfminは、あてはめたモデルに対するカイ2乗の自由度。
CFIの詳細については、Bentler（1990）を参照してください。
RNI
相対非心度指標（RNI; Relative Noncentrality Index）は次のように定義されます。
RNI = 
ここで
は、独立モデルに対するカイ2乗。
df0は、独立モデルに対するカイ2乗の自由度。
は、あてはめたモデルに対するカイ2乗。
dfminは、あてはめたモデルに対するカイ2乗の自由度。
RNIの詳細については、McDonald and Marsh（1990）を参照してください。
TLI
TLI（Tucker-Lewis Index; Tucker-Lewis指標）の定義は、以下のとおりです。
TLI = 
ここで
は、独立モデルに対するカイ2乗。
df0は、独立モデルに対するカイ2乗の自由度。
は、あてはめたモデルに対するカイ2乗。
dfminは、あてはめたモデルに対するカイ2乗の自由度。
詳細については、West et al.（2012）を参照してください。
NFI
Bentler-BonettのNFI（Normed Fit Index; 規準化適合指標、標準化適合指標）の定義は以下のとおりです。
NFI = 
ここで
は、独立モデルに対するカイ2乗。
は、あてはめたモデルに対するカイ2乗。
詳細については、West et al.（2012）を参照してください。
Revised GFIとRevised AGFI
修正済みGFI（revised Goodness-of-Fit Index）の定義は以下のとおりです。
Revised GFI = 
ここで
は、あてはめたモデルに対するカイ2乗。
dfminは、あてはめたモデルに対するカイ2乗の自由度。
pは、あてはめたモデルの観測変数の個数。
nは、標本サイズ。
修正済みAGFI（revised Adjusted Goodness-of-fit Index）の定義は以下のとおりです。
Revised AGFI = 
ここで
p*は、観測変数の共分散行列と平均ベクトルにおける要素の個数（ただし、共分散行列にて重複するものはカウントしない）。
dfminは、あてはめたモデルに対するカイ2乗の自由度。
詳細については、Maiti and Mukherjee（1991）およびWest et al.（2012）を参照してください。
RMSEA
近似の平均平方誤差平方根（RMSEA; Root Mean Square Error of Approximation）は次のように定義されます。
RMSEA = 
ここで
nは、標本サイズ。
dfminは、あてはめたモデルに対するカイ2乗の自由度。
は、あてはめたモデルに対するカイ2乗。
RMSEAの信頼限界は、非心カイ2乗分布の累積分布関数を使って計算されます（F(x|l, d)）。90%の信頼区間は、以下のように計算されます。
下限 = 
上限 = 
ここで
lLは、F(
|lL, dfmin) = 0.95を満たすもの。
lUは、F(
|lU, dfmin) = 0.05を満たすもの。
詳細については、Maydeu-Olivares et al.（2017）を参照してください。
RMRとSRMR
RMRとSRMRの計算式は、以下のとおりです。
RMR = 
SRMR = 
ここで
pは、顕在変数の個数。
bは、観測変数の共分散行列と平均ベクトルにおける要素の個数（ただし、共分散行列にて重複するものはカウントしない）。
sijは、入力データの共分散行列の(i, j)番目の要素。
は、推定された共分散行列の(i, j)番目の要素。
は、標本平均ベクトルのi番目の要素。
は、推定された平均ベクトルのi番目の要素。
詳細については、SAS Institute Inc.（2023a）の「CALIS Procedure」章を参照してください。