LSV 계산

LSV(최소 유의값)는 단일 선형 대비에 대해서만 계산됩니다.

단일 선형 대비 검정

자유도가 1인 Lb = 0 검정을 가정해 봅니다. 여기서 L은 상수로 구성된 행 벡터입니다. 이 가설에 대한 t-검정의 검정 통계량은 다음과 같습니다.

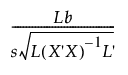
여기서 s는 제곱근 평균 제곱 오차입니다. 검정 통계량의 절대값이 자유도가 오차 자유도와 같은 t 분포의 1 - a/2 분위수(t1-α/2)를 초과하는 경우 유의 수준 a에서 가설이 기각됩니다.

(Lb)LSV로 표시되는 최소 유의값을 찾으려면 Lb 값을 구합니다.

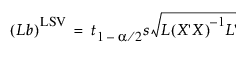
단일 모수 검정

선형 대비가 단일 bi를 0으로 설정하는 가설을 검정하는 특수한 경우에는 계산식이 다음과 같이 축소됩니다.

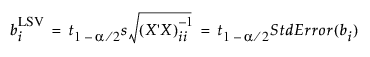
평균의 차이 검정

두 그룹의 평균을 비교하는 검정에 관심이 있는 경우 문헌에서 LSD(최소 유의차)에 대한 설명을 참조하십시오. 모형에 명목형 변수 하나만 포함된 특수한 경우 단일 선형 대비 검정을 위한 계산식이 LSD 계산식으로 축소됩니다.

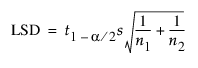
그러나 JMP에서 명목형 효과의 수준과 관련된 모수는 해당 수준의 평균과 모든 수준의 평균 간의 차이를 측정합니다. 따라서 이러한 비교에 대한 LSV는 평균 차이에 대한 LSD의 절반입니다.

참고: 명목형 효과 수준에서 대비를 검정하는 경우 JMP가 명목형 효과를 코드화하는 방식에 유의하십시오. 즉, 주어진 수준과 관련된 모수는 모든 수준의 평균에 대한 차이를 측정합니다.

더 많은 정보를 원하십니까? 질문이 있습니까? JMP 사용자 커뮤니티에서 답변 받기 (community.jmp.com).