아레니우스 가속 고장 로그 정규 모형의 예
이 예에서는 모수 생존 모형 적합 플랫폼을 사용하여 가열 스트레스가 가해진 유닛의 고장 시간에 분포를 적합시킵니다. 이 스트레스는 충분한 고장 데이터를 얻도록 유닛이 더 빨리 고장 나게 합니다.
1. 도움말 > 샘플 데이터 폴더를 선택하고 Reliability/Devalt.jmp를 엽니다.
먼저 이변량 플랫폼에서 시간에 대한 로그 척도를 사용하여 시간 대 온도 그림을 확인합니다.
2. 분석 > X로 Y 적합을 선택합니다.
3. Hours를 선택하고 Y, 반응을 클릭합니다.
4. Temp를 선택하고 X, 요인을 클릭합니다.
5. 확인을 클릭합니다.
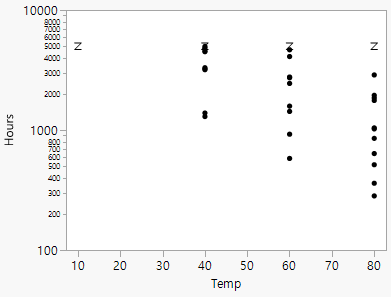
그림 15.7 Hours 대 Log Temp의 이변량 그림
이제 생존 플랫폼을 사용하여 각 온도에 대한 데이터의 로그 정규 확률도를 생성합니다.
6. 분석 > 신뢰성 및 생존 > 생존을 선택합니다.
7. Hours를 선택하고 Y, 사건 발생 시간을 클릭합니다.
8. Censor를 선택하고 중도절단을 클릭합니다.
9. Temp를 선택하고 그룹화를 클릭합니다.
10. Weight를 선택하고 빈도를 클릭합니다.
11. 확인을 클릭합니다.
12. Alt 키를 누른 채 "승법 극한 생존 적합" 옆의 빨간색 삼각형을 클릭합니다.
팁: Alt 키를 사용하면 여러 개의 빨간색 삼각형 메뉴를 동시에 선택할 수 있습니다.
13. 로그 정규 확률도와 로그 정규 적합을 선택합니다.
14. 확인을 클릭합니다.
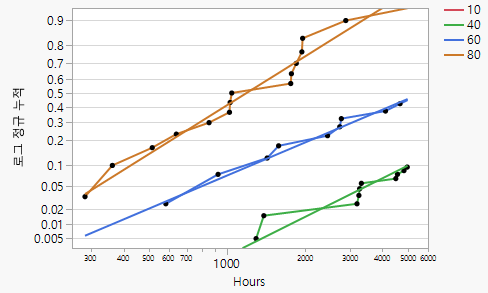
그림 15.8 로그 정규 확률도
이제 모수 생존 모형 적합 플랫폼에서 온도 효과를 사용하여 하나의 모형을 적합시킵니다.
15. 분석 > 신뢰성 및 생존 > 모수 생존 모형 적합을 선택합니다.
16. Hours를 선택하고 사건 발생 시간을 클릭합니다.
17. x를 선택하고 추가를 클릭합니다.
18. Censor를 선택하고 중도절단을 클릭합니다.
19. Weight를 선택하고 빈도를 클릭합니다.
20. 분포 유형을 로그 정규로 변경합니다.
21. 실행을 클릭합니다.
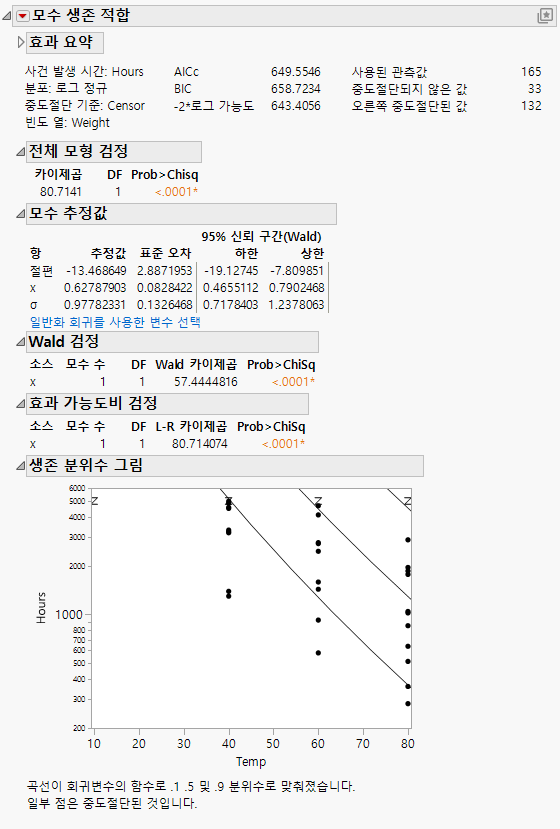
그림 15.9 Devalt 모수 출력
결과는 데이터의 회귀 적합을 보여 줍니다.
– 효과가 하나만 있고 연속형인 경우 효과의 함수로 나타낸 생존 그림이 표시됩니다. 0.1, 0.5 및 0.9 생존 확률에 선이 있습니다.
– 이 경우와 같이 효과 열에 다른 한 열의 계산식이 있는 경우 내부 열에 대한 그림이 표시됩니다. 이 예에서 효과는 x 열이지만 x의 함수인 Temp에 대한 그림이 표시됩니다.
마지막으로 30000 및 10000 시간에 대해 섭씨 10도의 온도로 외삽된 생존 확률 추정값을 구합니다.
22. "모수 생존 적합"의 빨간색 삼각형을 클릭하고 생존 확률 추정을 선택합니다.
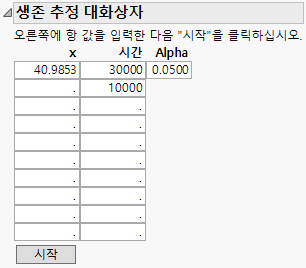
23. Figure 15.10에 표시된 값을 "생존 추정 대화상자"에 입력합니다.
10도의 아레니우스 변환은 40.9853(효과 값)입니다.
그림 15.10 생존 확률 추정
24. 시작을 클릭합니다.
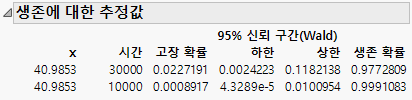
그림 15.11 생존 확률
"생존 추정값" 보고서에는 추정값과 신뢰 구간이 표시됩니다.