시간 ID 열 생성의 예
이 예에서는 시간 ID에 적절한 새 열을 생성한 후 시계열 플랫폼을 사용하여 시계열 분석을 수행합니다.
적절한 시간 ID 열 생성
1. 도움말 > 샘플 데이터 폴더를 선택하고 Time Series/SeriesP.jmp를 엽니다.
SeriesP.jmp 데이터 테이블에는 반응이 관측된 기간을 식별하는 Year 열과 Quarter 열이 포함되어 있습니다. 그러나 시계열 플랫폼에서 X 축에 라벨을 지정하려면 일정 간격의 고유한 시점이 포함된 하나의 열이 필요합니다. 시간 ID를 지정하지 않으면 행 번호를 사용하여 기간을 식별합니다. 이를 방지하고 보고서를 더 쉽게 해석하기 위해 Year 및 Quarter에서 시간 ID 열을 생성합니다.
2. 열 > 새 열을 선택합니다. "열 이름" 상자에 Year.Quarter를 입력합니다.
3. "형식" 옆에서 최적 > 날짜 > yyyyQq를 선택합니다.
4. 열 특성 > 계산식을 선택합니다.
5. "날짜/시간" 옆의 회색 삼각형을 클릭하고 Informat을 클릭합니다.
6. "문자" 옆의 회색 삼각형을 클릭합니다.
7. Year를 선택하고 Char, Concat를 차례로 클릭합니다.
8. 상자에 "Q"(인용 부호 포함)를 입력하고 Enter 키를 누릅니다.
9. Concat를 클릭합니다.
10. Quarter를 선택하고 Char을 클릭합니다.
11. <formatName> 상자를 클릭하고 yyyyQq를 입력한 후 Enter 키를 누릅니다.
12. 확인을 클릭합니다.
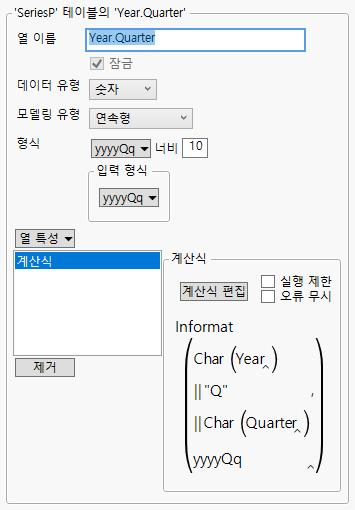
Figure 18.16에 나오는 것과 같은 완료된 "새 열" 창이 나타납니다.
그림 18.16 새 열
13. 확인을 클릭합니다.
참고: 이 시간 열은 X11 분석에도 사용됩니다.
시계열 분석
데이터 테이블에 적절한 시간 ID 열이 포함되었으므로 분석을 진행합니다.
1. 분석 > 전문 모델링 > 시계열을 선택합니다.
2. GDP를 선택하고 Y, 시계열을 클릭합니다.
3. Year.Quarter를 선택하고 X, 시간 ID를 클릭합니다.
4. 확인을 클릭합니다.
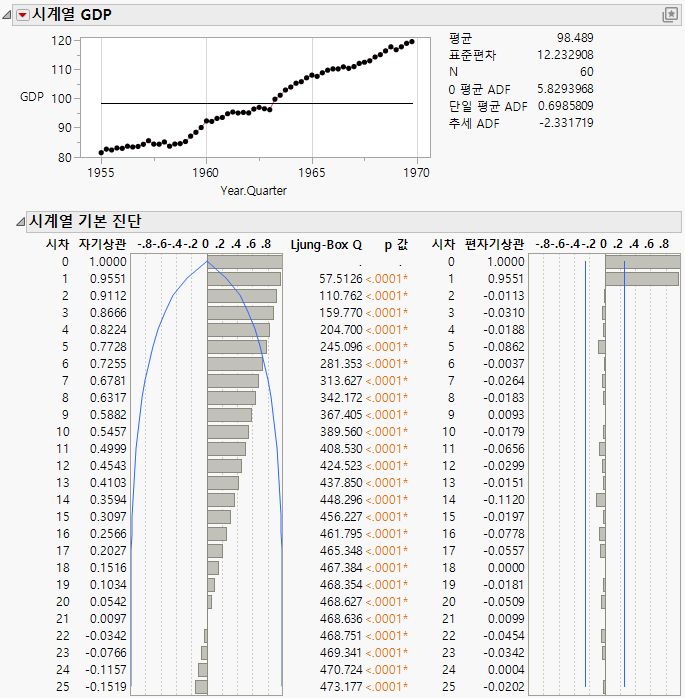
그림 18.17 SeriesP.jmp에 대한 시계열 보고서
계열은 시간이 지남에 따라 선형에 가까운 증가 추세를 보입니다. 또한 자기상관 차트에서는 서로 가까운 점 사이에 강한 상관관계가 있음을 보여 줍니다. 시차가 1, 2, 3인 점의 자기상관 값은 각각 0.9551, 0.9112, 0.8666입니다.
5. "시계열 GDP"의 빨간색 삼각형을 클릭하고 차분을 선택합니다.
6. "비계절 차분 차수"에 대해 "1"을 선택하고 추정을 클릭합니다.
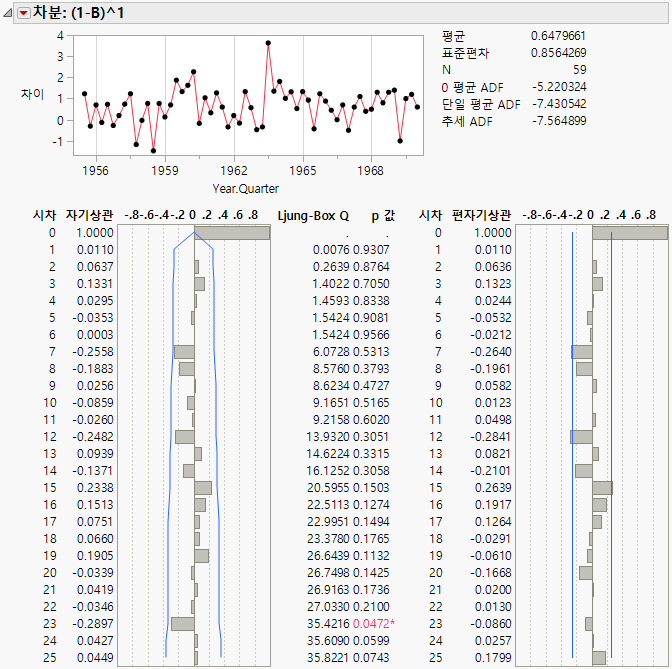
그림 18.18 SeriesP.jmp에 대한 차분 보고서
"차분" 보고서는 원래 시계열에 적합시킬 적절한 모형을 결정하는 데 도움이 됩니다. 차분 그림에서는 차분 계열에 원래 데이터에서 관측된 추세가 더 이상 없음을 보여 줍니다. 이는 시차-1 차분이 적절한 선택임을 나타냅니다. 또한 추세를 제거한 후에도 계열에 계절성 징후가 보이지 않습니다. 이러한 이유로 원래 계열을 적합시키는 모형은 선형 추세를 처리할 수 있어야 하지만 계절성을 반드시 처리할 필요는 없습니다. 선형 지수 평활 및 ARIMA 모형이 적절합니다.
7. "시계열 GDP"의 빨간색 삼각형을 클릭하고 평활 모형 > 선형 지수 평활을 선택합니다.
8. 추정을 클릭합니다.
9. "시계열 GDP"의 빨간색 삼각형을 클릭하고 ARIMA 모형 그룹을 선택합니다. 이렇게 하면 (p,d,q)(P,D,Q)의 값 범위에 대해 여러 ARIMA 모형을 적합시킬 수 있습니다.
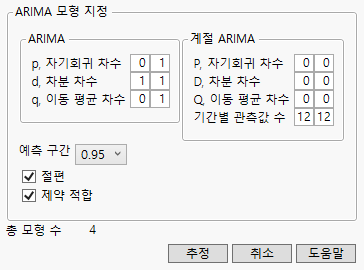
10. "ARIMA" 상자에서 다음 범위를 설정합니다.
– 차분 보고서에서 시차-1 차분이 적절하다는 것을 확인했으므로 1 ~ 1 범위를 설정하여 "d, 차분 차수"를 1로 수정합니다.
– 원래 계열에 자기상관 증거가 보였으므로 "p, 자기회귀 차수"를 0 ~ 1 범위로 설정합니다.
– "Q, 이동 평균 차수"를 0 ~ 1 범위로 설정합니다.
참고: 대부분의 경우 p와 q를 작게 유지하면 충분합니다.
– 계열에 계절성 증거가 없었으므로 P, D, Q는 설정된 값(0) 그대로 둡니다.
이러한 설정을 통해 총 네 개의 모형이 적합됩니다.
그림 18.19 ARIMA 모형 그룹 규격
11. 추정을 클릭합니다.
그림 18.20 모형 비교 테이블
모형 비교 테이블은 AIC 기준에 따라 최량 적합 모형이 목록의 맨 위에 오도록 정렬됩니다. 이 경우 보고서에 "I(1)"로 표시된 ARIMA(0,1,0) 모형이 원래 시계열에 가장 적합합니다. 또한 I(1) 모형이 "최량" 모형이지만 모든 모형의 적합 통계량 값이 매우 비슷하다는 점도 유의해야 합니다. 모두 적절하다고 간주할 수 있습니다.
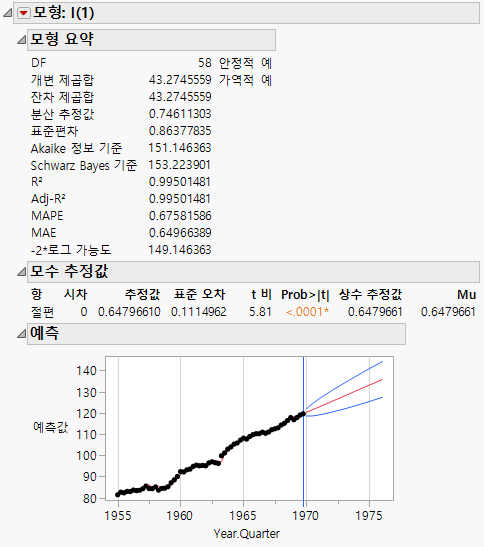
그림 18.21 ARIMA(0,1,0)에 대한 모형 보고서
I(1) 모형 보고서에는 예측 그래프가 표시됩니다. 파란색 선은 예측 구간을 나타냅니다. GDP는 선형 비율로 계속 증가한다고 예측됩니다.