Weibull 손실 함수 적합의 예
이 예에서 모형은 비선형 플랫폼의 Weibull, 로그 정규 및 지수 분포를 사용하여 생존 시간에 적합됩니다. 모형 적합에는 두 가지 효과만 있는 단순 생존 모형, 모든 효과가 있는 더 복잡한 모형, 완전 모형에 포함할 이산 효과 Cell Type에 대한 가변수 생성이 포함됩니다.
비선형 모형 적합은 모형 모수에 제공하는 초기값의 영향을 받는 경우가 많습니다. 이 예에서 적절한 초기값을 찾는 한 가지 방법은 먼저 비선형 플랫폼을 사용하여 선형 모형만 적합시키는 것입니다. 모형이 수렴되면 모수의 해 값이 비선형 모형의 초기 모수 값이 됩니다.
1. 도움말 > 샘플 데이터 폴더를 선택하고 VA Lung Cancer.jmp를 엽니다.
첫 번째 모형과 모든 손실 함수는 이미 데이터 테이블에 계산식으로 생성되어 있습니다. Model 열의 계산식은 다음과 같습니다.
Log(:Time) - (b0 + b1 * Age + b2 * Diag Time)
2. 분석 > 전문 모델링 > 비선형을 선택합니다.
3. Model을 선택하고 X, 예측변수 계산식을 클릭합니다.
4. 확인을 클릭합니다.
5. 시작을 클릭합니다.
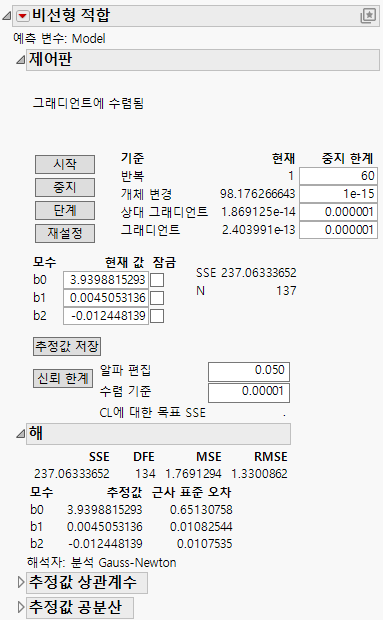
그림 15.24 비선형 적합 제어판의 초기 모수 값
보고서에서는 이 모형에 대한 최소 제곱 모수 추정값을 계산합니다.
6. 추정값 저장을 클릭합니다.
열 계산식의 모수 추정값은 이 초기 비선형 적합 프로세스에 의해 추정된 값으로 설정됩니다.
Weibull 열에는 Weibull 계산식이 포함됩니다. 자세한 내용은 Weibull 손실 함수의 신뢰성 및 생존 방법에서 확인하십시오.
적합 프로세스를 계속하려면 다음을 수행하십시오.
7. 분석 > 전문 모델링 > 비선형을 다시 선택합니다.
8. Model을 선택하고 X, 예측변수 계산식을 클릭합니다.
9. Weibull loss를 선택하고 손실을 클릭합니다.
10. 확인을 클릭합니다.
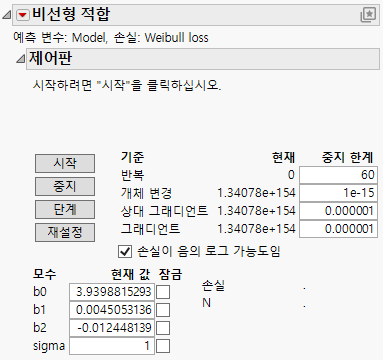
그림 15.25 초기 비선형 적합 제어판
이제 손실 함수에 sigma라는 모수가 추가되었습니다. 이것은 분수의 분모에 있으므로 시작 값 1이 sigma에 적절합니다. 기본값 이외의 손실 함수를 사용하는 경우 "제어판"의 손실이 음의 로그 가능도임 상자가 기본적으로 선택됩니다.
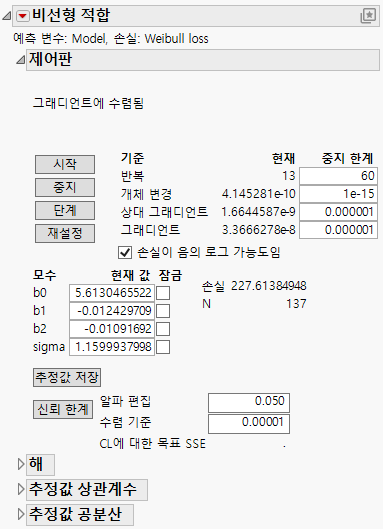
11. 시작을 클릭합니다.
그림 15.26 비선형 적합
적합 프로세스는 Weibull 가능도 함수의 음의 로그를 최대화하여 모수를 추정합니다.
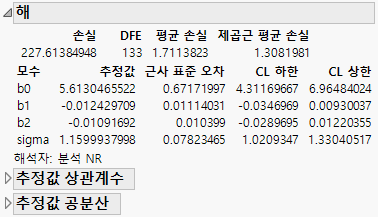
12. (선택 사항) 신뢰 한계를 클릭하여 "해" 테이블의 모수에 대한 95% 신뢰 하한 및 상한을 표시합니다.
그림 15.27 해 보고서
참고: 신뢰 한계는 표준 점근적 신뢰 구간이 아니라 프로파일 가능도 신뢰 구간이므로 계산하는 데 시간이 걸릴 수 있습니다.
사전 정의된 지수 및 로그 정규 손실 함수를 사용하여 모형을 실행할 수도 있습니다. 다른 모형을 적합시키기 전에 모수 추정값을 최소 제곱 추정값으로 재설정합니다. 그렇지 않으면 모수 추정값이 수렴되지 않을 수 있습니다. 모수 추정값을 재설정하려면 다음을 수행하십시오.
13. (선택 사항) "비선형 적합"의 빨간색 삼각형을 클릭하고 원래 모수로 되돌리기를 선택합니다.