비모수 Wilcoxon 검정의 예
일원 분석 플랫폼에서 Wilcoxon 검정을 사용하여 회사의 평균 수익이 회사 유형에 따라 다른지 여부를 확인합니다. 데이터는 제약 회사(12개)와 컴퓨터 회사(20개)라는 두 가지 회사 유형에 대한 다양한 측정 기준으로 구성되어 있습니다.
1. 도움말 > 샘플 데이터 폴더를 선택하고 Companies.jmp를 엽니다.
2. 분석 > X로 Y 적합을 선택합니다.
3. Profits ($M)를 선택하고 Y, 반응을 클릭합니다.
4. Type을 선택하고 X, 요인을 클릭합니다.
5. 확인을 클릭합니다.
6. "일원 분석"의 빨간색 삼각형을 클릭하고 표시 옵션 > 상자 그림을 선택합니다.
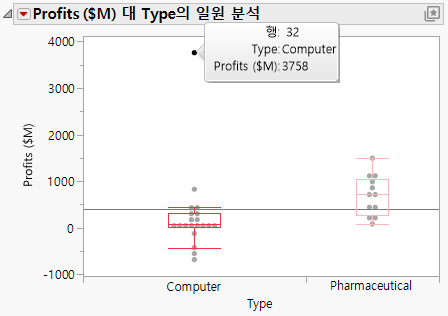
그림 6.22 컴퓨터 회사의 수익 분포
상자 그림을 보면 그룹 내의 수익 분포가 정규 분포를 따르거나 대칭이 아님을 알 수 있습니다. 32행 회사의 경우에는 모수 검정에 영향을 줄 수 있는 매우 큰 값이 있습니다.
7. "일원 분석"의 빨간색 삼각형 메뉴를 클릭하고 비모수 > Wilcoxon/Kruskal-Wallis 검정을 선택합니다.
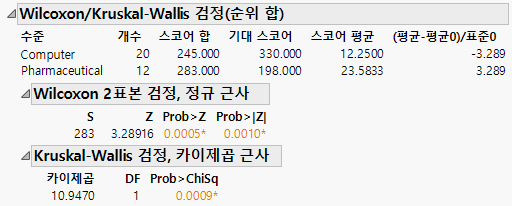
그림 6.23 Wilcoxon 검정 결과
0.5 연속성 수정을 사용하는 정규 근사와 Wilcoxon 검정 통계량에 대한 카이제곱 근사는 모두 0.0010 이하의 p 값에서 유의성을 나타냅니다. 따라서 분포의 이 위치에서 유의한 차이가 있으며 회사 유형에 따라 평균 수익에 차이가 있다는 결론을 내릴 수 있습니다.
정규 검정과 카이제곱 검정은 검정 통계량의 점근적 분포를 기반으로 합니다. 정확 검정도 수행할 수 있습니다.
8. "일원 분석"의 빨간색 삼각형 메뉴를 클릭하고 비모수 > 정확 검정 > Wilcoxon 정확 검정을 선택합니다.
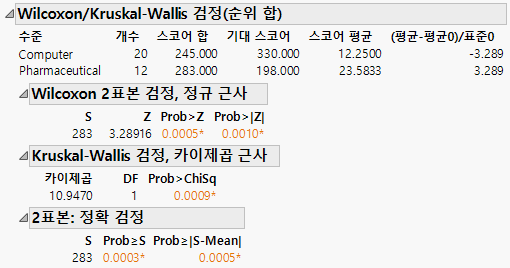
그림 6.24 Wilcoxon 정확 검정 결과
관측된 검정 통계량 값은 S = 283입니다. 이는 표본 크기가 더 작은 Type 수준(Pharmaceutical)의 순위 합입니다. 평균 중간 순위와의 절대 차이가 S의 절대값에서 중간 순위의 평균을 뺀 값을 초과하는 것으로 관측될 확률은 0.0005입니다. 이는 위치의 차이에 대한 양측 검정으로, 회사 유형별로 수익이 다르지 않다는 가설을 기각할 것을 지지합니다.
이 예에서는 비모수 검정이 정규성 기반 ANOVA 검정 또는 이분산 t-검정보다 더 적절합니다. 비모수 검정은 32행에 있는 큰 값의 영향을 받지 않으며 정규성 가정이 필요하지 않습니다.