지수, Weibull 및 로그 정규 그림과 적합
생존 플랫폼에서 지원되는 세 가지 분포에 대해 각각 그림 명령과 적합 명령이 있습니다. 그림 명령을 사용하여 사건 표식이 직선을 따르는지 여부를 확인합니다. 표식은 분포 적합이 데이터에 적절할 때 직선을 따르는 경향이 있습니다. 그런 다음 적합 명령을 사용하여 모수를 추정합니다.
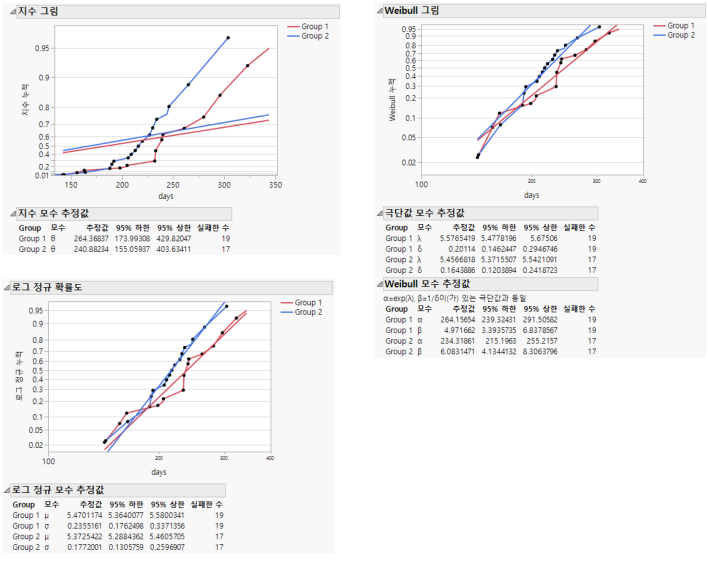
그림 14.5 지수, Weibull 및 로그 정규 그림과 보고서
다음 표에서는 해당 분포에 대한 직선 적합을 생성하기 위해 그림에 표시할 항목을 보여 줍니다.
분포 그림 | 가로 축 | 세로 축 | 해석 |
|---|---|---|---|
지수 | 시간 | -log(S) | 기울기 = 1/세타 |
Weibull | log(시간) | log(-log(S)) | 기울기 = 베타 |
로그 정규 | log(시간) | Probit(1-S) | 기울기 = 1/시그마 |
참고: S = 생존 분포의 승법 극한 추정값입니다.
지수
지수 분포는 사건 발생 시간 데이터를 모델링하기 위한 가장 간단한 분포입니다. 지수 분포에는 세타 모수 하나만 있습니다. 이 분포는 사건 발생 가능성에 영향을 미칠 때까지 생존한 기간에 대한 기억이 없는 상수 위험 분포입니다. 세타 모수는 기대 수명입니다.
Weibull
Weibull 분포는 사건 발생 시간 데이터를 모델링하는 데 가장 많이 사용되는 분포입니다. Weibull 분포에는 두 개 또는 세 개의 모수가 있을 수 있습니다. 생존 플랫폼에서는 2모수 Weibull 분포를 적합시킵니다. 작성자는 이 분포를 다양한 방법으로 파라미터화합니다(Table 14.2). JMP에서는 Weibull 알파-베타 파라미터화와 최소 극단값 분포 기반 파라미터화라는 두 가지 파라미터화를 보고합니다.
"Weibull 모수 추정값" 보고서에 표시된 알파-베타 파라미터화는 신뢰성 문헌에서 널리 사용됩니다(Nelson 1990). 알파 모수는 유닛의 63.2%가 고장 나는 분위수로 해석됩니다. 베타 모수는 시간 경과에 따라 위험률이 어떻게 변하는지를 결정합니다. 베타 > 1이면 시간 경과에 따라 위험률이 증가하고, 베타 < 1이면 시간 경과에 따라 위험률이 감소하며, 베타 = 1이면 시간 경과에 따라 위험률이 일정합니다. 위험 함수가 상수인 Weibull 분포는 지수 분포와 동일합니다.
람다-델타 극단값 파라미터화는 "극단값 모수 추정값" 보고서에 표시됩니다. 이 파라미터화는 위치-척도 설정에 Weibull 분포를 사용하므로 때때로 통계적 의미에서 바람직합니다(Meeker & Escobar 1998, p. 86). 위치 모수는 람다이고 척도 모수는 델타입니다. 알파-베타 파라미터화와 비교하여 람다는 알파의 자연 로그와 같고 델타는 베타의 역수와 같습니다. 따라서 델타 모수는 시간 경과에 따라 위험률이 어떻게 변하는지를 결정합니다. 델타 > 1이면 시간 경과에 따라 위험률이 감소하고, 델타 < 1이면 시간 경과에 따라 위험률이 증가하며, 델타 = 1이면 시간 경과에 따라 위험률이 일정합니다. 위험 함수가 상수인 Weibull 분포는 지수 분포와 동일합니다.
JMP Weibull | 알파 | 베타 |
Wayne Nelson | alpha=알파 | beta=베타 |
Meeker & Escobar | eta=알파 | beta=베타 |
Tobias & Trindade | c = 알파 | m = 베타 |
Kececioglu | eta=알파 | beta=베타 |
Hosmer & Lemeshow | exp(X beta)=알파 | lambda=베타 |
Blishke & Murthy | beta=알파 | alpha=베타 |
Kalbfleisch & Prentice | lambda = 1/알파 | p = 베타 |
JMP 극단값 | lambda=log(알파) | delta=1/베타 |
Meeker & Escobar s.e.v. | mu=log(알파) | sigma=1/베타 |
로그 정규
로그 정규 분포도 사건 발생 시간 데이터를 모델링하는 데 많이 사용됩니다. 로그 정규 분포는 값에 로그를 취할 경우 정규 분포를 따르는 분포와 동일합니다. 데이터에 정규 분포를 적합시키려면 exp()를 사용하여 로그 정규 분포로 데이터를 모델링할 수 있습니다. 자세한 내용은 모수 생존 모형 적합의 추가 예에서 확인하십시오.
추가 옵션
지수, Weibull 및 로그 정규 적합에 대한 추가 옵션을 보려면 Shift 키를 누르고 "승법 극한 생존 적합" 옆의 빨간색 삼각형을 클릭한 후 원하는 적합을 선택합니다.
이러한 옵션을 사용하여 다음 작업을 수행할 수 있습니다.
• 한계의 신뢰 수준을 설정합니다.
• 세타(지수 적합의 경우), 시그마(로그 정규 적합의 경우) 또는 베타(Weibull 적합의 경우)에 대한 제약 값을 설정합니다. 자세한 내용은 WeiBayes 분석에서 확인하십시오.
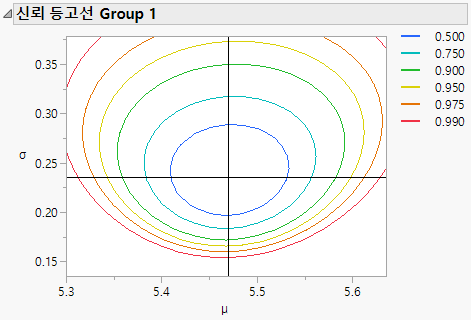
• Weibull 및 로그 정규 적합에 대한 신뢰 등고선 그림을 생성합니다(제약 값이 없는 경우).
그림 14.6 신뢰 등고선 그림
WeiBayes 분석
JMP에서는 이러한 분포를 적합시킬 때 세타(지수), 베타(Weibull) 및 시그마(로그 정규) 모수의 값을 제한할 수 있습니다. 이 기능은 다음과 같은 WeiBayes 상황에서 필요합니다.
• 고장이 거의 또는 전혀 없는 경우
• 베타에 대한 기존 과거 값이 있는 경우
• 알파를 추정해야 하는 경우
WeiBayes 상황에 대한 자세한 내용은 Abernethy(1996)에서 확인하십시오.
고장이 없는 경우 표준 기법은 끝에 고장을 추가하는 것입니다. 그러면 추정값에 실제 추정값이 아니라 알파 값의 하한 유형이 반영됩니다. 그러나 WeiBayes 기능을 사용하면 실제 추정이 가능합니다.