CI 길이의 증가 비율
"설계 평가" 보고서에 CI 길이의 증가 비율이 보고됩니다. CI 길이의 증가 비율은 현재 설계에서 제공한 모수 신뢰 구간의 길이를 이상적 설계에서 제공한 신뢰 구간의 길이와 비교합니다.
• 모수에 대한 이상적인 신뢰 구간의 길이를 실제 신뢰 구간의 길이에서 뺍니다.
• 이 차이를 이상적 신뢰 구간의 길이로 나눕니다.
직교 D-최적 설계의 경우 증가 비율이 0입니다. 설계를 선택할 때 신뢰 구간 길이의 증가 비율을 가능한 한 작게 하려고 합니다.
이상적 설계
보통 최소 제곱 추정량의 공분산 행렬은 s2(X¢X)-1입니다. (X¢X)-1의 대각 요소는 모수 추정값의 상대 분산(분산을 s2으로 나눈 값)입니다. 2수준 설계에서 효과 코드화 규칙(코딩 참조)을 사용할 경우 모수 추정값에 대한 상대 분산의 최소값은 1/n입니다. 여기서 n은 런 수입니다. 이는 설계의 모든 효과가 직교이고 설계가 D-최적일 때 해당됩니다.
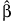가 모수 추정값의 벡터라고 하면 이상적 설계(존재하지 않을 수 있음)는 공분산 행렬이 다음과 같이 지정된 설계입니다.
여기서 In은 n x n 단위 행렬이고 s는 반응의 표준편차입니다.
직교 D-최적 설계가 존재하면 해당 설계가 이상적입니다. 그러나 위의 정의는 이상적 설계의 개념을 직교와 D-최적을 모두 충족하는 설계가 존재하지 않는 상황으로 확장합니다.
이 정의는 여러 수준의 범주형 요인이 있는 설계에도 적합합니다. 범주형 요인에 사용되는 직교 코드화를 통해 이러한 설계가 이상적 공분산 행렬을 가질 수 있습니다. 사용자 설계의 경우 "사용자 설계" 창의 옵션에서 "행렬 X 저장"을 선택하고, 설계 테이블을 생성한 다음, 설계 테이블에 저장된 "모형 행렬" 스크립트를 확인하면 코딩 행렬을 볼 수 있습니다.
신뢰 구간 길이의 증가 비율
이상적 설계에서 모수 추정값의 표준 오차는 다음과 같이 지정됩니다.
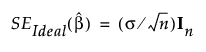
신뢰 구간 길이는 표준 오차에 의해 결정됩니다. 신뢰 구간 길이의 증가 비율은 주어진 설계의 표준 오차와 이상적 설계의 표준 오차 간 차이를 이상적 설계의 표준 오차로 나눈 값입니다.
i번째 모수 추정값의 경우 신뢰 구간 길이의 증가 비율은 다음과 같이 정의됩니다.
다음은 각 요소에 대한 설명입니다.
s2 은 알려지지 않은 반응 분산입니다.
X는 주어진 설계의 모형 행렬이며, 별칭 행렬에 정의되어 있습니다.
은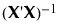 
의 i번째 대각 항목입니다.
n은 런 수입니다.