신뢰 한계를 사용한 역추정 예측
역추정 예측은 반응 값에서 독립 변수의 값을 추정합니다. 생물학적 분석 문제의 경우 신뢰 한계를 사용한 역추정 예측이 특히 유용합니다. JMP에서는 연속형 및 이항 반응 모형에 대한 역추정 예측 추정값을 요청할 수 있습니다. 반응이 연속형인 경우 개별 반응 또는 기대 반응에 대한 신뢰 한계를 요청할 수 있습니다.
신뢰 한계는 다음 논리를 기반으로 한 Fieller의 정리(1954)를 사용하여 계산됩니다. 다른 회귀변수 및 반응 값이 주어지면 단일 회귀변수의 값과 신뢰 한계를 예측하는 것이 목표입니다.
• b가 b 모수를 추정하여 b가 N(b,V) 분포를 따르도록 합니다.
• x를 관심 있는 회귀변수 값으로 합니다(i번째 값 추정).
• y를 반응 값으로 합니다.
다른 모든 x 값이 주어질 때 b¢x = y가 되는 x[i] 값에 대한 신뢰 영역에 관심이 있습니다.
역추정 예측은 다음과 같습니다.
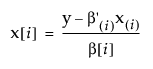
여기서 괄호 안의 첨자 (i)는 i번째 성분이 생략되었음을 나타냅니다. 다음과 같은 관계에서 신뢰 구간을 구성할 수 있습니다.

여기서 t는 지정된 신뢰 수준에 대한 t 값입니다.
다음 방정식은

z = x[i]에 따라 2차로 작성할 수 있습니다.
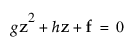
다음은 각 요소에 대한 설명입니다.
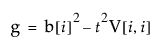
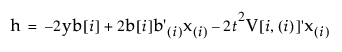
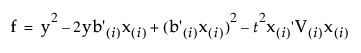
g, h 및 f 값에 따라 부등식을 충족하는 값 집합 및 역추정 예측의 신뢰 구간은 다음과 같은 여러 형식을 가질 수 있습니다.
• f1 < f2 조건에서 (f1, f2) 형식의 구간
• f1 < f2 조건에서 (-¥, f1) È (f2, ¥) 형식의 겹치지 않는 두 구간
• 전체 실직선 (-¥, ¥)
• -(¥, f) 또는 (f, ¥) 중 하나만
Fieller 신뢰 구간이 확장된 실직선인 경우 Wald 구간이 제공됩니다.
참고: X로 Y 적합 로지스틱 플랫폼 및 모형 적합 명목형 로지스틱 분석법에서는 역추정 예측을 위한 신뢰 구간을 계산할 때 t 값을 사용합니다. 모형 적합 일반화 선형 모형 분석법 및 SAS/STAT의 PROC PROBIT에서는 서로 다른 결과를 제공하는 z 값을 사용합니다.