적합 결여
"최소 제곱 적합" 보고서의 "적합 결여" 옵션은 모형이 데이터를 잘 적합시키는지 여부를 평가하는 검정의 상세 정보를 제공합니다. "적합 결여" 보고서는 이 검정을 수행할 수 있을 때만 나타납니다. 이 검정은 모형에 독립적인 추정값을 사용하여 반응의 분산을 추정할 수 있는지가 관건입니다. 이 추정값을 생성하려면 모형 효과의 반복된 값에서 반응 값을 사용할 수 있어야 합니다. 검정에는 이러한 반복된 관측값을 사용하여 제곱합을 기반으로 순수 오차 추정값을 계산하는 과정이 포함됩니다.
다음 상황에서는 검정 통계량을 계산할 수 없으므로 "적합 결여" 보고서가 나타나지 않습니다.
• X 변수에 대해 반복된 점이 없어 순수 오차 제곱합을 계산할 수 없는 경우
• 모형이 포화되어 추정 모수가 관측값 수만큼 있는 경우. 이러한 모형은 완벽하게 적합되므로 적합 결여를 평가할 수 없습니다.
모형의 오차 제곱합과 순수 오차 제곱합 사이의 차이를 적합 결여 제곱합이라고 합니다. 모형이 적절하지 않은 경우 적합 결여 변동이 순수 오차 변동보다 매우 클 수 있습니다. 예를 들어 예측 변수의 함수 형태가 잘못되었거나, 모형의 교호작용이 충분하지 않거나 올바르지 않을 수 있습니다.
"적합 결여" 보고서에는 다음 열이 포함됩니다.
소스
변동의 소스로는 적합 결여, 순수 오차 및 총 오차의 세 가지가 있습니다.
DF
각 오차 소스의 DF(자유도)입니다.
– 총 오차의 DF는 분산 분석 테이블의 오차 행에 나오는 DF 값과 같습니다. 총 오차 DF는 제곱합 분해를 기반으로 적합 결여의 자유도와 순수 오차의 자유도로 분할됩니다.
– 순수 오차 DF는 반복된 각 관측값 그룹에서 풀링된 것입니다. 일반적으로 g개의 그룹이 있고 각 그룹이 각 효과에 대해 동일한 설정을 갖는 경우 순수 오차 DF, 즉 DFPE는 다음과 같이 정의됩니다.
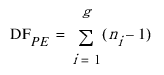
여기서 ni는 i번째 그룹의 반복 실험 수입니다.
– 적합 결여 DF는 총 오차 DF와 순수 오차 DF 사이의 차이입니다.
제곱합
각 오차 소스에 대한 관련 SS(제곱합)입니다.
– 총 오차 SS는 해당 분산 분석 테이블의 오차 행( 참조)에 나오는 제곱합입니다.
– 순수 오차 SS는 반복된 각 관측값 그룹에 대한 제곱합 값의 총계입니다. 순수 오차 SS를 DF로 나눈 값은 지정된 예측 변수 설정에서 반응의 분산을 추정합니다. 이 추정값은 모형의 영향을 받지 않습니다. 일반적으로 g개의 그룹이 있고 각 그룹이 각 효과에 대해 동일한 설정을 갖는 경우 순수 오차 SS, 즉 SSPE는 다음과 같이 정의됩니다.
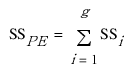
여기서 SSi는 관측된 각 반응과 i번째 그룹의 평균 반응 간의 차이에 대한 제곱합입니다.
– 적합 결여 SS는 총 오차 제곱합과 순수 오차 제곱합 사이의 차이입니다.
평균 제곱
소스의 평균 제곱, 즉 제곱합을 DF로 나눈 값입니다. 순수 오차 평균 제곱에 비해 적합 결여 평균 제곱이 크면 모형이 잘 적합되지 않음을 나타냅니다. F 비는 공식 검정을 제공합니다.
F 비
적합 결여의 평균 제곱 대비 순수 오차의 평균 제곱에 대한 비율입니다. F 비는 적합 결여 및 순수 오차 평균 제곱에 의해 추정된 분산이 동일하다는 가설, 즉 "적합 결여 없음"을 나타내는 것으로 해석되는 가설을 검정합니다.
Prob > F
적합 결여 검정의 p 값입니다. p 값이 작으면 적합 결여가 유의함을 나타냅니다.
최대 R²
이러한 효과만 기반으로 한 모형에서 얻을 수 있는 최대 R²입니다. 순수 오차 제곱합은 모형 형태에 따라 변동되지 않습니다. 따라서 이러한 반복된 효과가 있는 모형에서 설명할 수 있는 최대 변동은 다음과 같습니다.
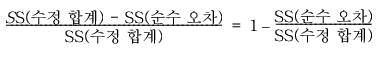
이 계산식은 최대 R²을 정의합니다.