일반화 선형 모형 분석법 시작

분석 > 모형 적합을 선택하고 Y에 대해 하나 이상의 열을 입력한 후 분석법 메뉴에서 일반화 선형 모형을 선택하여 일반화 선형 모형 분석법을 시작합니다.

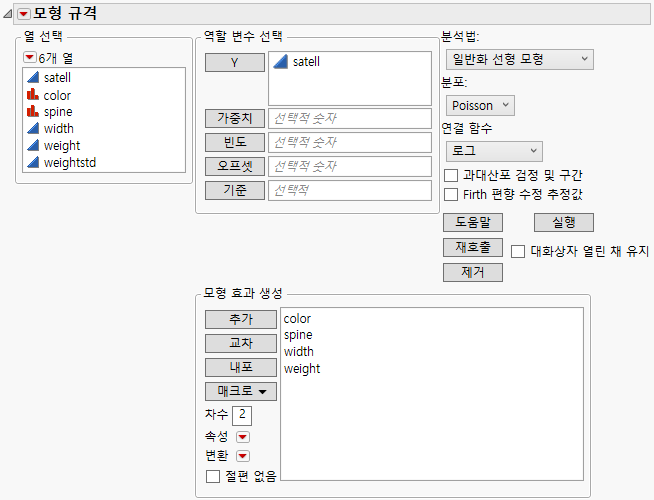
그림 13.4 일반화 선형 모형이 선택된 모형 적합 시작 창 

"모형 적합" 창에서 모든 분석법에 공통된 요소에 대한 자세한 내용은 모형 규격에서 확인하십시오. "열 선택"의 빨간색 삼각형 메뉴에 포함된 옵션에 대한 자세한 내용은 JMP 사용의 열 필터 메뉴에서 확인하십시오. 여기에서는 일반화 선형 모형 분석법에 대한 정보를 제공합니다.

모형 효과에 결측값이 있는 경우 이러한 결측값을 정보 범주로 처리할 수 있습니다. "모형 규격"의 빨간색 삼각형 메뉴에서 "결측값 정보화" 옵션을 선택합니다.

팁: 모형 적합 플랫폼의 일반화 선형 모형 분석법에서는 "절편 없음" 옵션을 사용할 수 없습니다.

"분석법"에서 "일반화 선형 모형"을 선택하면 모형 적합 시작 창이 변경되어 추가 옵션을 포함합니다. 일반화 선형 모형 분석법에서는 다음 추가 옵션을 사용할 수 있습니다.

분포

반응 변수에 대한 확률 분포를 지정합니다.

연결 함수

선형 모형을 반응 변수와 관련짓는 연결 함수를 지정합니다.

과대산포 검정 및 구간

과대산포 모수가 모형에 포함되도록 지정합니다. 과대산포는 반응 분산이 반응 분포의 이론적 분산에 의해 예상되는 것보다 클 때 발생합니다. Poisson 및 이항 반응 모형에서 과대산포가 발생할 수 있습니다. McCullagh and Nelder 연구 자료(1989)에 따르면 과대산포는 실제로 흔히 일어나는 일입니다.

참고: 이 옵션은 "전체 모형 검정" 보고서의 "적합도 통계량" 테이블에 "과대산포" 열을 추가합니다.

Firth 편향 수정 추정값

Firth 편향 수정 방법을 사용하여 모형을 적합시키도록 지정합니다. 이 최대 가능도 기반 방법은 편향 수정을 사용하지 않는 최대 가능도 기반 모형보다 더 나은 추정값과 검정을 생성하는 것으로 나타났습니다. 또한 편향 수정된 MLE는 로지스틱 유형의 모형에서 발생하기 쉬운 분리 문제도 개선합니다. 로지스틱 회귀의 분리 문제에 대한 자세한 내용은 Firth 연구 자료(1993) 및 Heinze and Schemper 연구 자료(2002)에서 확인하십시오.

오프셋

(역할 변수 선택 버튼으로 표시됨) 오프셋 변수를 지정합니다. 오프셋 변수는 모수가 1.0으로 고정된 회귀 공변량처럼 처리되는 변수입니다. 오프셋 변수는 로그 연결을 사용하는 Poisson 회귀에서 평균의 모델링을 척도화하는 데 가장 자주 사용됩니다.

이항 반응 분포의 반응 지정

"분포"에서 "이항"을 선택하면 다음 방법 중 하나를 사용하여 반응 변수를 지정해야 합니다.

• 데이터가 사건 빈도로 요약되지 않은 경우 단일 이진 열을 반응으로 지정합니다. 반응 열은 명목형이어야 합니다.

• 데이터가 사건 빈도로 요약된 경우 단일 이진 열을 반응으로 지정하고 "빈도" 역할에 빈도 변수를 지정합니다. 반응 열은 명목형이어야 하고 빈도 변수는 각 반응 수준의 수를 포함합니다.

• 데이터가 사건 빈도 및 시행 횟수로 요약된 경우 성공 횟수-시행 횟수의 순으로 두 개의 연속형 열을 지정합니다. 성공 횟수 대신 실패 횟수를 지정할 수도 있습니다.