가능도, AICc 및 BIC
JMP의 많은 통계 모형은 최대 가능도라는 기법을 사용하여 적합됩니다. 이 기법은 가능도 함수를 최대화하여 모형의 모수를 추정합니다. 이 섹션에서는 모형의 모수를 b로 표시합니다. L(b)로 표시되는 가능도 함수는 관측된 데이터 값에서 평가된 확률 밀도 함수 또는 확률 질량 함수(이산형 분포의 경우)의 곱입니다. 최대 가능도 추정은 관측된 데이터가 주어지면 모수 b에 대해 L(b)을 최대화하는 값을 찾습니다.
가능도 함수 L(b)을 최대화하는 것보다 가능도 함수의 음의 자연 로그 -Log L(b)을 사용하는 것이 더 편리합니다. L(b) 최대화 문제는 음의 로그 가능도를 최소화하려는 최소화 문제로 다시 작성됩니다(-1*로그 가능도 = -Log L(b)). 따라서 음의 로그 가능도 값이 더 작거나 음의 로그 가능도의 두 배(-2*로그 가능도)인 경우 모형이 더 적합하다는 것을 나타냅니다.
음의 로그 가능도 값을 사용하여 모형을 선택하고 JMP의 여러 플랫폼에서 생성된 모형 적합을 비교하는 사용자 가설 검정을 수행할 수 있습니다. 이 작업은 가능도비 검정을 사용하여 수행됩니다. 여러 JMP 플랫폼에서 -2*로그 가능도가 보고되는 한 가지 이유는 완전 모형과 축소 모형 -2*로그 가능도 값의 차이가 점근적으로 카이제곱 분포를 따르기 때문입니다. 이 가능도비 검정과 관련된 자유도는 두 모형의 모수 수 차이와 같습니다(Wilks 1938).
수정 AICc(Akaike 정보 기준) 및 BIC(베이지안 정보 기준)는 정보를 기반으로 모형 적합을 평가하는 기준입니다. 둘 다 -2*로그 가능도를 기반으로 합니다.
AICc는 다음과 같이 정의됩니다.
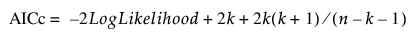
여기서 k는 모수의 수(회귀 계수 및 오차의 표준편차 포함)이고 n은 모형에 사용된 관측값 수입니다. 이 값은 동일한 데이터 집합에 대한 여러 모형을 비교하여 가장 적합한 모형을 결정하는 데 사용할 수 있습니다. Akaike(1974)에 설명된 대로 값이 가장 작은 모형이 일반적으로 선호됩니다.
BIC는 다음과 같이 정의됩니다.
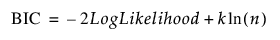
여기서 k는 모수의 수(회귀 계수 및 오차의 표준편차 포함)이고 n은 모형에 사용된 관측값 수입니다. 두 모형의 BIC 값을 비교할 때 BIC 값이 작은 모형이 더 나은 것으로 간주됩니다.
일반적으로 BIC는 모수 수가 많은 모형에 AICc보다 벌점을 더 많이 부과합니다. 이러한 이유로 AICc와 비교하여 더 간결한 모형, 즉 모수 수가 더 적은 모형을 선택하게 됩니다. AICc와 BIC의 자세한 비교는 Burnham and Anderson 연구 자료(2004)에서 확인하십시오.
최소 제곱 회귀의 단순화된 AICc 및 BIC 계산식
최소 제곱 회귀의 경우 AICc 및 BIC를 SSE(오차 제곱합)에 따라 계산할 수도 있습니다. SSE를 기준으로 AICc 및 BIC는 다음과 같이 정의됩니다.
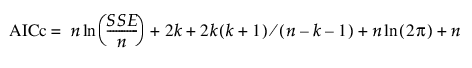
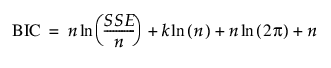
여기서 k는 모수의 수(회귀 계수 및 오차의 표준편차 포함), n은 모형에 사용된 관측값 수, SSE는 모형의 오차 제곱합입니다.