명목형 반응
모형 적합 플랫폼에서 명목형 반응은 로짓 모형의 간단한 확장을 통해 분석됩니다. 이항(2수준) 반응의 경우 로짓 반응 모형은 다음과 같이 지정됩니다.
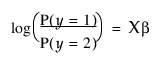
위의 모형을 다음과 같이 작성할 수도 있습니다.

여기서 F(x)는 표준 로지스틱 분포의 누적 분포 함수입니다.
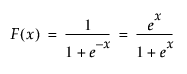
반응 수준이 r개인 경우 JMP는 반응이 데이터 값에 의해 주어진 r개의 여러 반응 수준 중 하나일 확률을 적합시킵니다. 확률 추정값은 모두 양수여야 합니다. 주어진 X 구성에 대해 확률 추정값의 합은 전체 반응 수준에서 1이어야 합니다. JMP에서 확률을 예측하는 데 사용되는 함수는 선형 모형과 다중 반응 로지스틱 함수의 합성입니다. 확률 비율의 로그가 선형 모형이므로 로그 선형 모형이라고도 합니다. JMP는 각 반응 확률을 r번째 확률과 관련짓고, 별도의 설계 모수 집합을 이러한 r - 1개 모형에 적합시킵니다.
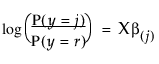 단,
단, 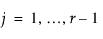
명목형 반응의 적합 원칙
이 적합 원칙을 최대 가능도라고 합니다. 이 방법은 데이터에 의해 제공된 모든 반응의 결합 확률이 모형에서 얻을 수 있는 최대값이 되도록 모수를 추정합니다. 결합 확률(가능도)을 직접 보고하는 것보다 가능도의 음의 로그 합계를 보고하는 것이 관리하기가 더 쉽습니다.
불확도(음의 로그 가능도)는 모형이 표본 데이터에서 실제로 발생한 반응에 기인한 확률의 음의 로그 합입니다. 이 값은 크기가 n인 표본에 대해 H로 표시되고 다음과 같이 작성됩니다.
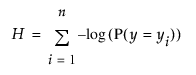
확률 1을 발생한 각 사건에 기인한 것으로 볼 경우 완벽한 적합을 위한 음의 로그 합은 0입니다.
명목형 모형, 특히 반응 수준이 많은 모형을 적합시키려면 시간 및 메모리가 많이 소요될 수 있습니다. JMP는 음의 로그 가능도 값이 추정값에 수렴할수록 작아지는 것을 보여 주는 반복 기록을 사용하여 계산 진행 정도를 추적합니다.
명목형 반응의 기준 모형
명목형 반응에 대한 가장 단순한 모형은 전체 데이터 테이블에서 각 반응 수준에 대한 발생률로 적합된 일련의 상수 반응 확률입니다. 즉, y가 반응 수준 j일 확률은 총 표본 수 n을 각 반응 수준 nj의 총계로 나누어 추정됩니다. 이 확률은 다음과 같이 지정됩니다.
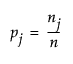
다른 모든 모형이 이 기준 모형과 비교됩니다. 명목형 반응에 대한 기준 모형은 연속형 모형에 대한 표본 평균과 동일하게 사용됩니다.
R2 통계량은 다음과 같이 모형에 의해 설명되는 불확도 비율을 측정합니다.

그러나 실제로 범주형 모형에 대해 R2이 1에 가까운 경우는 거의 없습니다.