요인 분석 플랫폼 개요
요인 분석은 더 적은 수의 관측 불가능한 요인의 관점에서 관측 가능 변수 집합을 모델링합니다. 요인은 관측 변수 간의 상관 또는 공분산을 설명하기 위해 구성됩니다. 요인의 해석력을 높이기 위해 요인 회전을 사용하여 요인의 기준 축을 변경할 수 있습니다.
10개의 관측 변수 X1, X2, …, X10이 있는 경우를 가정해 보겠습니다. 이러한 10개의 변수를 F1과 F2라는 두 잠재 요인의 관점에서 모델링하려고 합니다. 편의상 요인은 상관관계가 없으며 각 요인의 평균은 0, 분산은 1이라고 가정합니다. 도출하려는 모형의 형식은 다음과 같습니다.
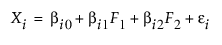
따라서 Var(Xi) = bi12 + bi22 + Var(ei)입니다. Xi의 분산 중 요인, 즉 공통 분산 또는 공통분으로 인한 부분은 bi12 + bi22입니다. 나머지 분산 Var(ei)는 고유 분산이며 Xi에 고유한 특정 분산과 오차 분산의 조합으로 간주됩니다.
이 플랫폼에서는 상관 행렬 또는 공분산 행렬의 고유값에 대한 스크리 그림을 제공합니다. 이 그림을 참고로 사용하여 추출할 요인 수를 결정할 수 있습니다. 플랫폼의 기본 요인 수는 1을 초과하는 고유값 수입니다.
이 플랫폼에서는 이 모형의 모수를 추정하기 위해 "주 축"과 "최대 가능도"라는 두 가지 요인화 방법을 제공합니다. 각 변수의 공통 요인이 기여하는 분산 비율을 추정하기 위한 두 가지 "사전 공통분" 옵션이 있습니다. 이러한 옵션은 상관 행렬 또는 공분산 행렬의 대각에 대한 가정을 설정합니다. "주성분" 옵션은 대각의 값이 1인 상관 행렬 또는 대각의 값이 분산인 공분산 행렬을 분석할 구조로 처리합니다. "공통 요인 분석" 옵션은 대각 항목을 SMC(다중상관제곱)로 설정합니다. 이러한 값은 다른 변수와 공유하는 변동 비율을 반영합니다.
요인 회전은 추출된 요인의 해석력을 뒷받침하는 데 사용됩니다. 요인 분석 플랫폼에서는 직교 회전과 사각 회전을 모두 포함하는 다양한 회전 방법을 제공합니다.
공통 분산을 고려하는 요인 분석과 달리 주성분 분석은 관측 변수의 총 분산을 설명합니다. 자세한 내용은 주성분에서 확인하십시오.
요인 분석에 대한 자세한 내용은 Jöreskog(1977) 또는 Cudeck과 MacCallum(2007) 연구 자료에서 확인하십시오.