Passing-Bablok 적합 보고서
이변량 플랫폼에서 "Passing-Bablok 적합" 옵션을 사용하여 Passing-Bablok 방법으로 회귀 모형을 적합시킵니다. Passing-Bablok 회귀는 두 가지 다른 분석 방법의 측정값을 비교하기 위해 개발되었습니다. 이 방법은 강한 상관관계가 있는 두 변수 간의 선형 관계를 가정합니다. 적합선 및 Y = X를 나타내는 점선이 산점도에 추가됩니다. "Passing-Bablok 적합"의 빨간색 삼각형 메뉴에서 "Bland Altman 분석" 옵션을 사용하여 쌍체 t-검정 및 Bland-Altman 분석을 수행합니다.
"Passing-Bablok 적합" 보고서에는 세 개의 테이블이 포함되어 있습니다.
비모수: Kendall t
Kendall t를 사용하여 X 변수와 Y 변수 간의 상관관계를 평가할 수 있습니다.
X
X 변수입니다.
Y
Y 변수입니다.
Kendall t
X 변수와 Y 변수 간의 비모수 상관 측도입니다. 값은 -1에서 1 사이이며, 값이 0에 가까우면 X 변수와 Y 변수 간의 독립성을 나타냅니다.
Prob>|t|
X 변수와 Y 변수 간의 독립성에 대한 가설 검정과 관련된 p 값입니다. p 값이 작으면 변수가 종속적이며 Passing-Bablok 방법이 적절하다는 것을 뒷받침합니다.
선형성에 대한 CUSUM 검정
"선형성에 대한 CUSUM 검정" 테이블에는 선형성 검정 결과가 포함됩니다. p 값이 작으면 선형성에 대한 귀무가설을 기각하여 Passing-Bablok 회귀가 적절하지 않을 수 있음을 나타냅니다.
최대 CUSUM
잔차의 부호를 기준으로 각 행에 할당되고 각 점에서 Passing-Bablok 선까지의 수직 거리에 따라 정렬되는 
및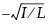 
값의 누적합 절대값의 최대값입니다. I는 양수 잔차를 갖는 관측값 수이고 L은 음수 잔차를 갖는 관측값 수입니다. 방법 간에 강한 상관관계가 있으면 I가 L과 같습니다. 따라서 누적합이 +1과 -1의 합인 경우가 종종 있습니다. CUSUM 값이 작으면 Passing-Bablok 선 양쪽에 점이 랜덤 분포되어 있음을 나타내고 이 결과는 선형성 가설을 뒷받침합니다.
H
CUSUM 검정에 대한 검정 통계량입니다. 이 검정 통계량은 최대 CUSUM을 음수 잔차 수 + 1의 제곱근으로 나누어 정의됩니다. 이 검정 통계량은 Kolmogorov-Smirnov 분포를 따릅니다.
Prob > H
CUSUM 검정의 p 값입니다. p 값이 작으면 Passing-Bablok 절차가 적절하지 않을 수 있음을 나타냅니다.
모수 추정값
"모수 추정값" 테이블에는 95% 신뢰 구간을 갖는 절편 및 기울기의 Passing-Bablok 적합 추정값이 포함됩니다.
매칭 쌍 보고서
"Passing-Bablok 적합"의 빨간색 삼각형 메뉴에서 "Bland Altman 분석" 옵션을 사용하여 쌍체 t-검정 및 Bland-Altman 분석을 수행합니다. 매칭 쌍에 대한 자세한 내용은 예측 및 전문 모델링의 매칭 쌍 분석에서 확인하십시오.
Bland-Altman 분석
"Bland-Altman 분석" 테이블에는 다음 모수에 대한 값, 표준편차 및 신뢰 한계가 포함됩니다.
편향
X 변수와 Y 변수 간의 평균 차이입니다.
합치도 한계
편향 ± z1-α/2*(편향의 표준편차)로 설정된 합치도 상한 및 하한입니다.