ANOVA에 대한 검정력
ANOVA에 대한 검정력 탐색기를 사용하면 ANOVA를 사용하여 분석할 k개의 그룹 또는 처리의 연구를 위해 표본 크기를 결정할 수 있습니다. DOE > 표본 크기 탐색기 > 검정력 > ANOVA에 대한 검정력을 선택합니다. 변동 가정, 표본 크기, 검정력 및 유의성 간의 균형을 탐색합니다. 표본 크기 및 검정력은 다음 가설 검정과 관련됩니다.
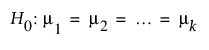
다음 양측 대립가설과 비교

다음은 각 요소에 대한 설명입니다.
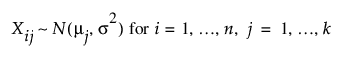
ANOVA에 대한 검정력 탐색기 옵션
라디오 버튼, 텍스트 상자 및 메뉴를 사용하여 연구 가정을 설정하고 표본 크기를 탐색합니다. 설정을 변경하면 프로파일러가 업데이트됩니다. 또는 프로파일러 곡선 위의 십자기호를 드래그하여 설정을 변경합니다.
검정 규격
가정할 통계량을 지정하는 옵션입니다.
그룹 평균
그룹 평균을 지정합니다(그룹 등분산 가정).
그룹 간 분산
그룹 간 분산을 지정합니다(그룹 등분산 가정).
최대 차이
감지할 최대 평균 차이를 지정합니다.
최악의 경우
다른 모든 평균이 동일하다는 가정하에 가장 큰 평균과 가장 작은 평균 사이의 최대 차이를 지정합니다.
하나를 제외한 전부
다른 모든 평균이 동일하다는 가정하에 한 평균과 다른 모든 평균 사이의 최대 차이를 지정합니다.
예비 정보
알파
제1종 오류의 확률, 즉 귀무가설이 참일 때 귀무가설을 기각할 확률을 지정합니다. 일반적으로 검정의 유의 수준이라고 합니다. 기본 유의 수준은 0.05입니다.
그룹 수
실험에 사용되는 그룹 또는 처리의 수를 지정합니다.
ANOVA에 대한 검정력 탐색기 프로파일러
프로파일러를 사용하면 표본 크기 가정이 검정력 계산에 미치는 영향을 시각화할 수 있습니다.
다음 값 계산:
표본 크기, 그룹 내 표준편차 또는 평균의 최대 차이를 계산할 수 있습니다.
검정력
귀무가설이 거짓일 때 기각할 확률을 지정합니다. 다른 모든 모수가 고정되면 표본 크기가 커질수록 검정력도 증가합니다.
표본 크기(그룹당)
실험의 각 그룹에 필요한 관측값(런, 실험 단위 또는 처리) 수를 지정합니다.
참고: 동일한 그룹 표본 크기만 지원됩니다.
그룹 내 분산(s2)
그룹 간 표준편차가 동일하다고 가정하는 경우 각 그룹의 가정된 모분산을 지정합니다.
그룹 평균
(검정 규격을 그룹 평균으로 설정한 경우에만 사용 가능) 가정된 그룹 평균을 지정합니다. 예비 정보에 지정된 각 그룹에 대해 프로파일러와 텍스트 상자가 하나씩 있습니다.
그룹 간 분산
(검정 규격을 그룹 간 분산으로 설정한 경우에만 사용 가능) 총 평균을 이루는 개별 그룹 평균의 분산을 지정합니다. 이 값은 K개 그룹에 대해 그룹 평균과 1/(K-1)로 척도화된 총 평균 사이의 차이에 대한 제곱합입니다.
평균의 최대 차이
(검정 규격을 최대 차이로 설정한 경우에만 사용 가능) 최고 극단 평균과 다른 모든 평균 사이의 최대 차이("하나를 제외한 전부") 또는 두 개의 최고 극단 평균 사이의 최대 차이("최악의 경우")를 지정합니다.
ANOVA에 대한 검정력 탐색기 옵션
탐색기의 빨간색 삼각형 메뉴와 보고서 버튼은 다음과 같은 추가 옵션을 제공합니다.
데이터 시뮬레이션
탐색기 설정을 기반으로 시뮬레이션된 데이터의 데이터 테이블을 엽니다. 사용된 설정에 대한 시뮬레이션된 반응 열 계산식을 봅니다.
데이터 수집 테이블 생성
데이터 수집에 사용할 수 있는 새 데이터 테이블을 생성합니다. 이 테이블에는 데이터 분석을 쉽게 할 수 있는 스크립트가 포함되어 있습니다.
설정 저장
현재 설정을 "저장된 설정" 테이블에 저장합니다. 이렇게 하면 일련의 대체 연구 계획을 저장할 수 있습니다. 자세한 내용은 표본 크기 탐색기의 저장된 설정에서 확인하십시오.
기본값으로 재설정
모든 모수와 그래프를 기본값으로 재설정합니다.
도움말
JMP 온라인 도움말을 엽니다.
ANOVA에 대한 검정력 탐색기의 통계 상세 정보
여러 그룹의 평균 간 차이를 검정하기 위한 검정력 계산에서는 각 그룹의 표준편차가 동일하다고 가정합니다. 검정력 계산은 표준 F-검정을 기반으로 합니다. 검정력(1-b)은 검정 규격을 기준으로 계산됩니다.
그룹 평균:
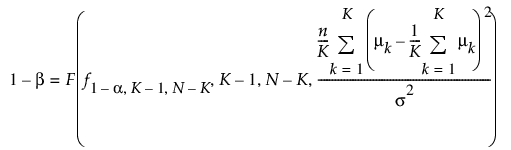
그룹 간:
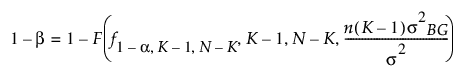
최대 차이(최악의 경우):
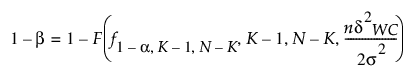
최대 차이(하나를 제외한 전부):
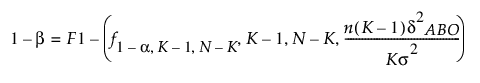
다음은 각 요소에 대한 설명입니다.
F(q, df1, df2, l)는 비중심성 모수 l를 갖는 비중심 F 분포입니다.
K는 그룹 수입니다.
n은 각 그룹 내의 표본 수입니다(모든 그룹에 대해 같다고 가정).
N = nK
mk는 그룹 k의 가정된 평균입니다.
s2BG는 그룹 평균과 1/(K-1)로 척도화된 총 평균 사이의 차이에 대한 제곱합입니다.
dWC는 가장 큰 그룹 평균과 가장 작은 그룹 평균 사이의 차이입니다.
dABO는 한 평균과 다른 모든 평균 사이의 차이입니다.
s2은 그룹 내 분산입니다(모든 그룹에 대해 같다고 가정).
a는 유의 수준입니다.