기저 함수 확장 모형 적합에 대한 통계 상세 정보

함수 데이터 탐색기 플랫폼의 일부 모형 적합은 기저 함수 확장에 의존합니다. 기저 함수는 독립 함수의 집합입니다. 함수 f(t)는 fk로 표시되는 K개 기저 함수의 선형 결합을 사용하여 근사화할 수 있습니다. 일반적으로 함수는 다음과 같이 근사화됩니다.

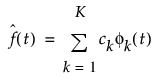
여기서 ck 모수는 기저 계수입니다. 평활 정도는 기저 함수의 수 K에 의해 결정됩니다. 기저 함수 확장에 대한 자세한 내용은 Ramsay and Silverman(2005) 연구 자료에서 확인하십시오.

Fourier 기저 모형

Fourier 기저를 정의하는 k = 1,..., K개 함수는 f0 = 1, f2k-1 = sin(rwt) 및 f2k = cos(rwt)가 되도록 정의됩니다. 그러면 근사 함수가 다음과 같이 정의됩니다.

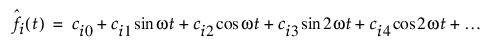
이는 A = 2p/w로 정의되는 주기 A를 갖는 주기 함수에 근사한 값을 산출합니다. 계수는 고정 기저 함수 계수와 함수별 랜덤 계수의 조합입니다. 각 c는 다음과 같이 정의됩니다.

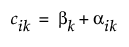
여기서 bk는 기저 함수 k의 고정 계수이고, aik는 특정 함수 공정 i에 대한 기저 함수 k의 랜덤 계수입니다. Fourier 기저 모형의 경우 bk 및 aik 모수의 추정값은 각각 "기저 함수 계수" 테이블과 "함수별 랜덤 계수" 테이블에서 확인할 수 있습니다.

Fourier 기저 모형에는 하나의 절편 항과 Fourier 쌍이라고 하는 동일한 수의 사인 항 및 코사인 항이 있습니다. 따라서 K는 항상 홀수입니다. 예를 들어 K = 7이면 절편 항 하나와 세 개의 Fourier 쌍이 있습니다.

더 많은 정보를 원하십니까? 질문이 있습니까? JMP 사용자 커뮤니티에서 답변 받기 (community.jmp.com).