거리 측도에 대한 통계 상세 정보
이 섹션에는 다변량 플랫폼의 이상치 분석 그림에 사용되는 거리 측도에 대한 통계 상세 정보가 포함되어 있습니다.
Mahalanobis 거리 측도
Mahalanobis 거리는 데이터의 상관 구조와 개별 척도를 고려합니다. 각 값에 대해 Mahalanobis 거리는 Mi로 나타내고 다음과 같이 계산됩니다.
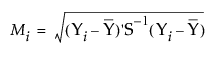
다음은 각 요소에 대한 설명입니다.
Yi = i번째 행의 데이터
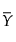= 평균 행
S = 데이터에 대한 추정된 공분산 행렬
"Mahalanobis 거리" 그림에 표시된 UCL 참조선(Mason과 Young 2002)은 다음과 같이 계산됩니다.
UCLMahalanobis =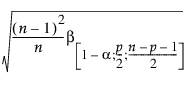 
다음은 각 요소에 대한 설명입니다.
n = 관측값 수
p = 변수(열) 수
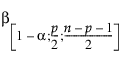= 베타 
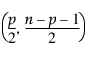분포의 (1–a)번째 분위수
변수가 다른 변수의 정확한 선형 결합인 경우 상관 행렬은 특이 행렬이고 해당 변수의 행과 열은 0으로 설정됩니다. 결과로 생성되는 일반화 역행렬은 거리를 구성하는 데 유효합니다.
잭나이프 거리 측도
잭나이프 거리는 관측값 자체를 포함하지 않는 평균, 표준편차 및 상관 행렬의 추정값을 사용하여 계산됩니다. 각 값에 대해 잭나이프 거리는 다음과 같이 계산됩니다.
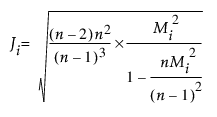
다음은 각 요소에 대한 설명입니다.
n = 관측값 수
p = 변수(열) 수
Mi = i번째 관측값의 Mahalanobis 거리
"잭나이프 거리" 그림에 표시된 UCL 참조선(Penny 1996)은 다음과 같이 계산됩니다.
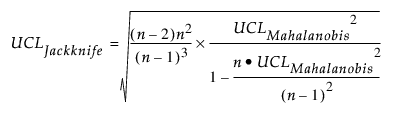
T2 거리 측도
T2 거리는 Mahalanobis 거리의 제곱이므로 Ti2 = Mi2입니다.
T2 거리의 UCL은 다음과 같습니다.
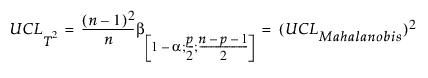
다음은 각 요소에 대한 설명입니다.
n = 관측값 수
p = 변수(열) 수
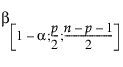= 베타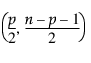 
분포의 (1–a)번째 분위수
다변량 거리는 여러 차원에서 이상치를 찾는 데 유용합니다. 그러나 변수가 다변량 관점에서 높은 상관관계가 있는 경우에는 점을 차원의 부분집합에서 비정상으로 보지 않고 다변량 공간의 이상치로 간주할 수 있습니다. 즉, 값이 상관되어 있는 경우 하나 또는 두 개의 축을 따라 보면 점이 특별하지 않을 수 있지만 상관관계를 위반하여 이상치가 될 수 있습니다.