분포에 대한 통계 상세 정보
이 섹션에는 수명 분포 플랫폼의 분포 적합에 대한 상세 정보가 포함되어 있습니다. 뒤에 나오는 비모수 및 모수 상세 정보 둘 다에 대한 이론, 적용 및 설명은 Meeker & Escobar(1998, ch. 2-5)에서 확인하십시오.
추정 및 신뢰 구간
다른 설명이 없는 한, 모든 분포의 모수는 MLE(최대 가능도 추정값)를 사용하여 추정됩니다. 임계 분포만 예외입니다. 최소 관측값이 정확 고장인 경우 이 관측값은 작은 구간으로 구간 중도절단되었다고 간주됩니다. 모수 추정값은 약간 수정된 이 데이터 집합에서 추정된 MLE입니다. 이 수정이 없으면 비유계 가능도가 될 수 있으므로 MLE가 없을 수 있습니다. 이 방법은 최소 정확 고장이 중도절단된다는 점만 제외하면 Meeker & Escobar(1998, p. 275)에 설명된 방법과 비슷합니다. 이는 가능도 함수의 유계성을 보장하는 최소 데이터 변화입니다.
수명 분포 플랫폼에서는 분포 모수에 대한 신뢰 구간을 계산하는 두 가지 방법을 제공합니다. 이러한 방법은 "Wald" 또는 "가능도" 라벨로 표시되며 수명 분포 플랫폼 시작 창에서 선택할 수 있습니다. Wald 신뢰 구간이 기본 설정으로 사용됩니다. cdf(누적 분포 함수)에 대한 신뢰 구간 계산은 표준화 변수에 대한 Wald 신뢰 구간으로 시작됩니다. 그런 다음 구간이 cdf 척도로 변환됩니다(Nelson 1982, pp. 332–333 및 pp. 346-347). 다른 그래프와 프로파일러에 제공되는 신뢰 구간은 변환된 Wald 구간입니다(Meeker & Escobar 1998, ch. 7). 2모수 분포의 모수에 대한 결합 신뢰 구간은 로그 가능도 등고선 그림에 표시됩니다. 이러한 구간은 모수에 대한 근사 가능도비를 기반으로 합니다(Meeker & Escobar 1998, ch. 8).
비모수 적합
비모수 적합은 분포의 기본 곡선을 나타냅니다. 중도절단이 없는 데이터(고장만 해당)와 관측값이 고장 및 오른쪽 중도절단으로 구성된 데이터의 경우 JMP에서 Kaplan-Meier 추정값이 사용됩니다. 혼합, 구간 또는 왼쪽 중도절단의 경우 Turnbull 추정값이 사용됩니다. 데이터 집합에 오른쪽 중도절단 데이터만 포함된 경우에는 "비모수 추정값" 보고서에 비모수 추정값을 계산할 수 없다는 내용이 표시됩니다.
수명 분포 플랫폼에서는 계단 함수의 중간점 추정값을 사용하여 확률도를 생성합니다. 중간점 추정값은 현재 Kaplan-Meier 추정값과 이전 Kaplan-Meier 추정값의 중간 또는 평균입니다.
모수 분포
모수 분포는 비모수 분포보다 더 간결한 분포 적합을 제공합니다. 고장 시간 추정값 분포도 더 평활합니다. 또한 모수 모형은 분포의 하위 또는 상위 꼬리에 대한 외삽(시간)에 유용합니다.
참고: 수명 분포 플랫폼의 많은 분포는 위치 및 척도로 파라미터화됩니다. 로그 정규 적합의 경우 중앙값도 제공됩니다. 임계 분포에는 임계 모수도 포함됩니다. 위치는 m, 척도는 s, 임계는 g에 해당합니다.
로그 정규
로그 정규 분포는 데이터 범위가 10의 여러 거듭제곱일 경우 고장 시간을 나타내는 데 흔히 사용됩니다. 보통 이 분포는 독립적이며 같은 분포를 따르는 다수의 작은 양수 확률 변수의 곱으로 간주됩니다. 데이터 값의 로그가 정규 분포를 따르는 것처럼 보일 때 적절합니다. 로그 정규 분포로 적절하게 모델링된 데이터의 예로는 병원 비용 데이터, 금속 피로 균열 성장 및 소독제에 노출된 박테리아의 생존 시간이 있습니다. 일반적으로 pdf 곡선은 강한 오른쪽 왜도가 특징입니다. 로그 정규 pdf 및 cdf는 다음과 같습니다.
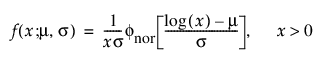
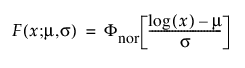
여기서,
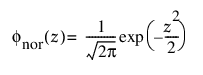
및
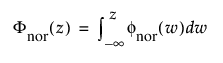
각각 표준화된 정규 또는 nor(m = 0, s = 1) 분포에 대한 pdf와 cdf입니다.
Weibull
Weibull 분포를 사용하면 위험률이 증가하거나 감소하는 고장 시간 데이터를 모델링할 수 있습니다. 형상 모수 b의 값을 기반으로 다양한 유형의 데이터를 모델링할 때 엄청난 유연성을 제공하므로 신뢰성 분석에 자주 사용됩니다. 이 분포는 전자 부품, 롤러 베어링, 콘덴서 및 세라믹의 고장을 설명하는 데 사용되고 있습니다. 척도 모수 a와 형상 모수 b를 변경하여 Weibull 분포의 다양한 모양을 나타낼 수 있습니다. 일반적으로 Weibull pdf와 cdf는 다음과 같이 나타냅니다.
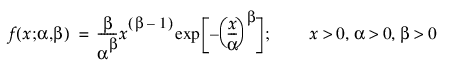
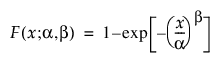
여기서 a는 척도 모수이고 b는 형상 모수입니다. Weibull 분포는 b = 1일 때 지수 분포로 축소되므로 융통성이 있습니다. 문헌과 JMP에서 자주 사용되는 대체 파라미터화는 s를 척도 모수로 사용하고 m를 위치 모수로 사용하는 것입니다. 이러한 모수는 다음 정의를 사용하여 a 및 b 파라미터화로 쉽게 변환됩니다.
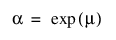
및
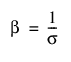
Weibull 분포의 pdf 및 cdf는 로그 변환된 SEV(최소 극단값) 분포로도 표현됩니다. 이 경우 m = log(a) 및 s = 1/b인 위치 척도 파라미터화를 사용합니다.
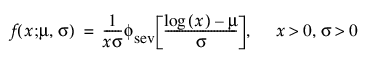
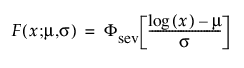
여기서,
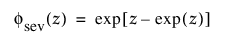
및
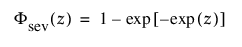
각각 표준화된 최소 극단값(m = 0, s = 1) 분포에 대한 pdf와 cdf입니다.
로그로지스틱
로그로지스틱 분포의 pdf는 로그 정규 분포와 모양이 비슷하지만 꼬리가 더 두껍습니다. 암 사망률 및 금융 자산과 같은 비단조 위험 함수를 나타내는 데이터를 모델링하는 데 주로 사용됩니다. 로그로지스틱 pdf와 cdf는 다음과 같습니다.
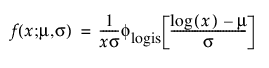
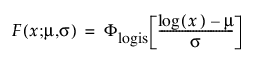
여기서,
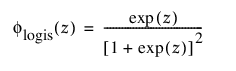
및
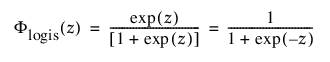
각각 표준화된 로지스틱 또는 logis(m = 0, s = 1) 분포에 대한 pdf와 cdf입니다.
Frechet
Frechet 분포는 로그-최대 극단값 분포라고 하며, Weibull 분포의 역수로 파라미터화될 때 최대값의 Frechet 분포라고도 합니다. 이 분포는 일반적으로 재무 데이터에 사용됩니다. pdf와 cdf는 다음과 같습니다.
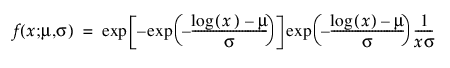
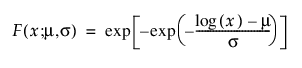
또한 다음과 같이 더 일반적으로 파라미터화됩니다.
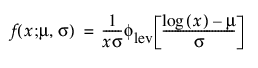
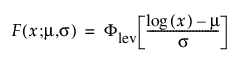
여기서,
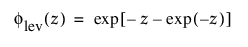
및
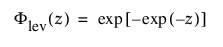
각각 표준화된 최대 극단값 LEV(m = 0, s = 1) 분포에 대한 pdf와 cdf입니다.
정규
정규 분포는 상대적으로 단순하고 중심 극한 정리를 쉽게 적용할 수 있기 때문에 대부분의 통계학 분야에서 가장 널리 사용되는 분포입니다. 그러나 신뢰성 분석에는 거의 사용되지 않습니다. 이 분포는 m > 0이고 변동 계수(s/m)가 작은 데이터에 가장 유용합니다. 위험 함수는 상한 없이 증가하므로 마모 고장을 나타내는 데이터에 특히 유용합니다. 예를 들면 백열 전구, 토스터 발열체, 와이어의 기계적 강도 등이 있습니다. pdf와 cdf는 다음과 같습니다.
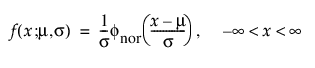
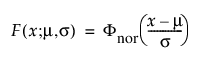
여기서,
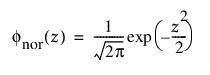
및
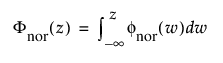
각각 표준화된 정규 또는 nor(m = 0, s = 1) 분포에 대한 pdf와 cdf입니다.
SEV(최소 극단값)
이 비대칭(왼쪽으로 편중) 분포는 두 가지 경우에 유용합니다. 첫 번째 경우는 데이터가 분포의 하위 꼬리 부분에 적은 수의 약한 유닛을 나타낼 때입니다(데이터가 많은 관측값 중 가장 작은 수를 나타냄). 두 번째 경우는 s가 m에 비해 작을 때입니다. SEV 분포를 사용할 경우 0보다 작을 확률이 적기 때문입니다. 최소 극단값 분포는 유닛이 오래될수록 위험률이 커지는 데이터를 설명하는 데 유용합니다. 예를 들면 노인 사망률과 가뭄 동안의 강수량이 있습니다. 이 분포를 Gumbel 분포라고도 합니다. pdf와 cdf는 다음과 같습니다.
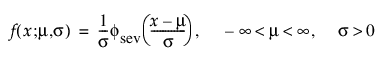
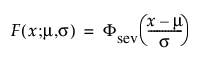
여기서,
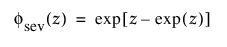
및
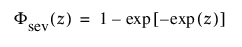
각각 표준화된 최소 극단값 SEV(m = 0, s = 1) 분포에 대한 pdf와 cdf입니다.
로지스틱
로지스틱 분포는 정규 분포와 모양이 비슷하지만 꼬리가 더 깁니다. 로지스틱 분포는 음수 고장 시간이 문제가 되지 않을 때 수명 데이터를 모델링하는 데 주로 사용됩니다. 이항 또는 순서형 반응에 대한 로지스틱 회귀 모형은 로지스틱 분포를 잠재 분포로 가정합니다. pdf와 cdf는 다음과 같습니다.
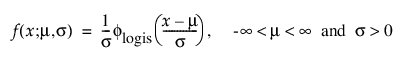
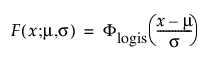
여기서,
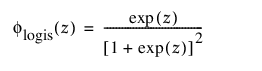
및
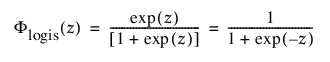
각각 표준화된 로지스틱 또는 logis(m = 0, s = 1) 분포에 대한 pdf와 cdf입니다.
LEV(최대 극단값)
오른쪽으로 편중된 이 분포는 s가 m > 0에 비해 작을 때 고장 시간을 모델링하는 데 사용할 수 있습니다. 이 분포는 일반적으로 신뢰성 분석에 사용되지 않지만 재난적 홍수 수위 또는 강풍 속도와 같은 극한 자연 현상을 추정하는 데 유용합니다. pdf와 cdf는 다음과 같습니다.
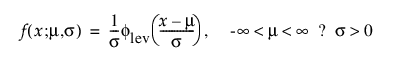
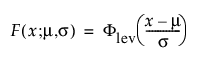
여기서,
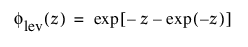
및
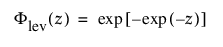
각각 표준화된 최대 극단값 LEV(m = 0, s = 1) 분포에 대한 pdf와 cdf입니다.
지수
1모수 지수 분포와 2모수 지수 분포 둘 다 신뢰성 분석에 사용됩니다. 2모수 지수 분포의 pdf와 cdf는 다음과 같습니다.
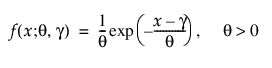
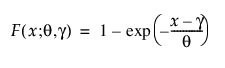
여기서, q는 척도 모수이고 g는 임계 및 위치 모수입니다. 신뢰성 분석에서는 g = 0인 1모수 지수 분포를 주로 사용합니다. 지수 분포는 기대 수명을 훨씬 초과한 마모를 나타내는 부품의 고장 시간을 설명하는 데 유용합니다. 이 분포는 고장 비율이 일정합니다. 즉, 시간 증분이 작은 경우 유닛의 고장은 유닛 수명과 관계가 없습니다. 피로, 부식 또는 단기 마모에 노출될 수 있는 기계 부품의 수명을 설명하는 데 지수 분포를 사용하면 안 됩니다. 그러나 이 분포는 특정 유형의 견고한 전자 부품을 모델링하는 데 적절합니다. 이 분포는 절연유 및 전기 비전도유체의 수명을 설명하는 데 사용되고 있습니다(Nelson 1990, p. 53).
로그 일반화 감마
로그 일반화 감마 분포에는 SEV, LEV 및 정규 분포가 포함됩니다. pdf와 cdf는 다음과 같습니다.
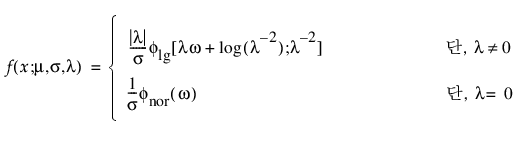
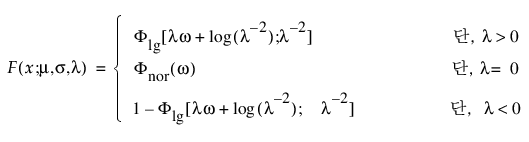
여기서, -¥ < x < ¥, w = [x – m]/s,
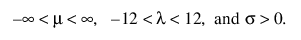
다음 사항에 유의하십시오.
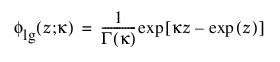
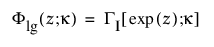
각각 로그-감마 변수에 대한 pdf와 cdf이며 k > 0은 형상 모수입니다. 위의 표준화된 분포는 형상 모수 k에 따라 달라집니다.
참고: JMP에서 일반화 감마 분포의 형상 모수 l는 수치 안정성을 제공하기 위해 [-12,12] 사이로 제한됩니다.
확장된 일반화 감마
확장된 일반화 감마 분포는 일반화 감마, Weibull, 로그 정규, Frechet, 감마 및 지수와 같은 다른 많은 분포를 특수 사례로 포함할 수 있습니다. 중도절단이 거의 또는 전혀 없는 경우에 특히 유용합니다. 이 분포는 암 환자의 예후를 모델링하는 데 사용되고 있습니다. pdf와 cdf는 다음과 같습니다.
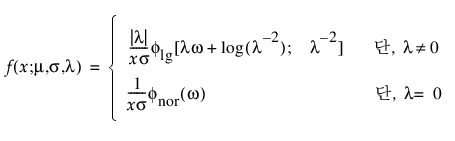
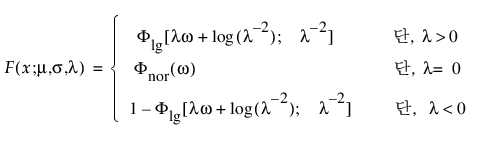
여기서, x > 0, w = [log(x) – m]/s,
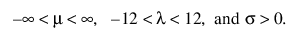
다음 사항에 유의하십시오.
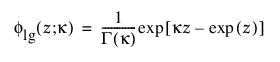
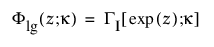
각각 표준화된 로그-감마 변수에 대한 pdf와 cdf이며 k > 0은 형상 모수입니다.
위의 표준화된 분포는 형상 모수 k에 따라 달라집니다. Meeker & Escobar(1998, ch. 5)에서는 확장된 일반화 감마 분포에 대한 자세한 설명을 제공합니다.
참고: JMP에서 일반화 감마 분포의 형상 모수 l는 수치 안정성을 제공하기 위해 [-12,12] 사이로 제한됩니다.
임계 모수가 있는 분포
임계 분포는 임계 모수가 있는 로그-위치-척도 분포입니다. 위의 분포 중 일부는 g로 표시되는 임계 모수를 추가하여 일반화됩니다. 이 임계 모수를 추가하면 왼쪽 끝점이 0에서 멀어집니다. 모든 유닛이 최소 임계 시간까지는 생존하기 때문에 임계 모수를 이동, 최소 또는 보증 모수라고도 합니다. 임계 모수를 추가하면 시간 축의 분포가 이동하지만 분포의 모양과 퍼짐에는 영향을 주지 않습니다. 임계 분포는 보통 또는 심하게 이동된 분포를 적합시키는 데 유용합니다. 로그-위치-척도 임계 분포의 pdf와 cdf에 대한 일반적 형식은 다음과 같습니다.
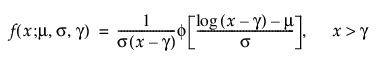
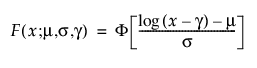
여기서, f와 F는 각각 특정 분포에 대한 pdf와 cdf입니다. Weibull, 로그 정규, Frechet 및 로그로지스틱 분포에 대한 특정 임계 분포의 예가 아래에 표시되어 있으며, 각각 SEV, 정규, LEV 및 logis pdf와 cdf가 적절하게 대체됩니다.
참고: 가장 작은 관측값이 고장(중도절단되지 않음)인 경우 JMP에서는 해당 점 주위에 작은 구간을 생성하고 관측값을 구간 중도절단된 것으로 처리합니다. 이렇게 고장 주변에 패딩을 추가하면 로그 가능도 함수의 경계가 설정되고 추정이 향상됩니다. 가장 작은 관측값이 중도절단된 경우에는 관측값에 별도의 패딩이 추가되지 않습니다.
TH Weibull
3모수 Weibull 분포의 pdf와 cdf는 다음과 같습니다.
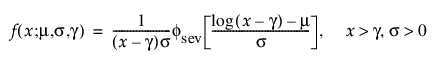
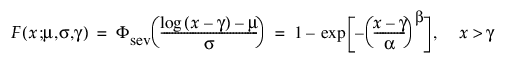
여기서, m =log(a), s= 1/b이고
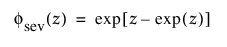
및
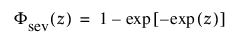
각각 표준화된 최소 극단값 SEV(m = 0, s = 1) 분포에 대한 pdf와 cdf입니다.
TH 로그 정규
3모수 로그 정규 분포의 pdf와 cdf는 다음과 같습니다.
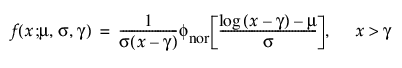
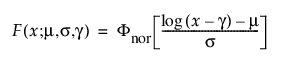
여기서,
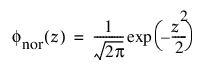
및
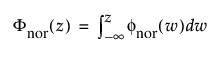
각각 표준화된 정규 또는 N(m = 0, s = 1) 분포에 대한 pdf와 cdf입니다.
TH Frechet
3모수 Frechet 분포의 pdf와 cdf는 다음과 같습니다.
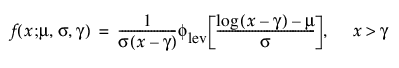
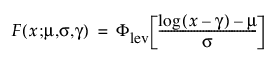
여기서,
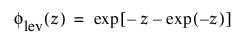
및

각각 표준화된 최대 극단값 LEV(m = 0, s = 1) 분포에 대한 pdf와 cdf입니다.
TH 로그로지스틱
3모수 로그로지스틱 분포의 pdf와 cdf는 다음과 같습니다.
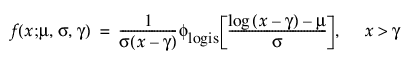
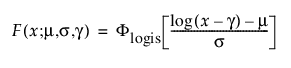
여기서,
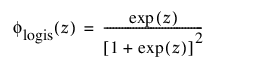
및
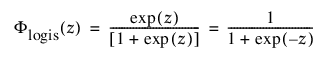
각각 표준화된 로지스틱 또는 logis(m = 0, s = 1) 분포에 대한 pdf와 cdf입니다.
결함 부모집단 분포
신뢰성 실험에서 고장 원인이 되는 특정 결함이 모집단의 일부에만 있을 때가 있습니다. 모든 유닛이 고장에 취약하지는 않으므로 정규 고장 분포를 사용하는 것은 적절하지 않고 잘못된 결과를 초래할 수 있습니다. 부모집단에서만 발생하는 고장을 모델링하려면 DS 분포 옵션을 사용합니다. 다음과 같은 DS 분포를 사용할 수 있습니다.
• DS 로그 정규
• DS Weibull
• DS 로그로지스틱
• DS Frechet
결함 부모집단 분포에 대한 pdf와 cdf는 다음과 같이 정의됩니다.
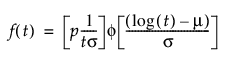
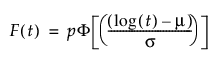
다음은 각 요소에 대한 설명입니다.
p - 결함 부모집단 비율
t - 수명 사건에 대한 측정 시간
m, s - 해당 결함 부모집단의 pdf와 cdf로 일반적인 최대 가능도 추정을 계산하여 추정됨
f(z), F(z) - 각각 표준 분포에 대한 밀도 및 누적 분포 함수. 예를 들어 Weibull 분포의 경우 다음과 같습니다.
f(z) = exp(z-exp(z)), F(z) = 1 - exp(-exp(z))
결함 부모집단 모형에 대한 자세한 내용은 Tobias & Trindade(2012, p. 321)에서 확인하십시오.
Meeker & Escobar(1998, ch. 11)에서는 결함 부모집단 모형을 limited failure population(제한된 고장 모집단) 모형이라고도 합니다.
영과잉 분포
영과잉 분포는 특정 비율(p)의 데이터가 t = 0에서 고장 나는 경우 사용됩니다. 데이터에 포함된 0이 표준 모형에서 예상한 것보다 많으면 0의 수가 부풀려집니다. 사건 발생 시간 데이터에 수명 분포 플랫폼의 최소값으로 0이 포함된 경우 네 개의 영과잉 분포를 사용할 수 있습니다. 여기에는 다음 분포가 포함됩니다.
• ZI 로그 정규(영과잉 로그 정규)
• ZI Weibull(영과잉 Weibull)
• ZI 로그로지스틱(영과잉 로그로지스틱)
• ZI Frechet(영과잉 Frechet)
영과잉 분포에 대한 pdf와 cdf는 다음과 같이 정의됩니다.
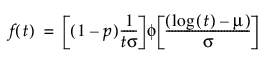
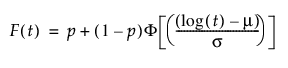
다음은 각 요소에 대한 설명입니다.
p - 0 데이터 값의 비율
t - 수명 사건에 대한 측정 시간
m, s - 원래 데이터에서 0 값을 제거한 후 일반적인 최대 가능도 추정을 계산하여 추정됨
f(z), F(z) - 각각 표준 분포에 대한 밀도 및 누적 분포 함수. 예를 들어 Weibull 분포의 경우 다음과 같습니다.
f(z) = exp(z-exp(z)), F(z) = 1 - exp(-exp(z))
영과잉 분포에 대한 자세한 내용은 Lawless(2003, p. 34)에서 확인하십시오. 위에 표시된 형식을 얻으려면 p = 1 - p, S1(t) = 1 - F(t)로 대체합니다.
신뢰성 분포에 대한 자세한 내용은 Tobias & Trindade(1995, p. 232)에서 확인하십시오. 이 참조 자료에서는 혼합 분포에 대한 일반적인 형식을 제공합니다. Tobias & Trindade의 파라미터화를 사용할 경우, a = p, Fd(t) = 1 및 FN(t) = F(t)로 대체하여 위의 형식을 얻을 수 있습니다.
베이지안 추정을 위한 사전 분포
다음은 위치 및 척도 사전 분포에 사용할 수 있는 분포입니다.
• Location(위치, mu) 및 Scale(척도, 시그마) 초모수가 있는 정규/로그 정규 분포. 정의는 로그 정규 및 정규에서 확인하십시오.
• 균등 분포의 받침을 정의하는 Low(하위) 및 End(끝) 초모수가 있는 균등 분포
• Shape(형상) 및 Scale(척도) 초모수가 있는 감마 분포. k/theta 파라미터화 및 확률 밀도 함수가 사용됩니다.
• Location(위치) 초모수가 있는 점질량 분포. 이는 퇴화된 사전 분포로, 사전 분포를 할당하는 모수에 사용 가능한 값이 하나뿐입니다. 가능한 값은 이 Location 초모수에 입력된 값과 같습니다.
다음은 분위수 및 모수 사전 분포에 사용할 수 있는 분포입니다.
• 99% 확률 범위로 분포의 0.005 및 0.995 백분위수를 사용하여 사전 분포를 지정하는 정규/로그 정규 분포. JMP는 mu와 시그마를 취소합니다.
• 균등 분포의 받침을 정의하는 Lower Limit(하한) 및 Upper Limit(상한) 초모수가 있는 균등 분포
• Lower Limit(하한, a) 및 Upper Limit(상한, b)가 있는 로그-균등 분포. 이 분포는 Log(a)와 Log(b) 사이의 로그 척도에서 균등합니다.
• Location(위치) 초모수가 있는 점질량 분포. 이는 퇴화된 사전 분포로, 사전 분포를 할당하는 모수에 사용 가능한 값이 하나뿐입니다. 가능한 값은 이 Location 초모수에 입력된 값과 같습니다.
다음은 고장 확률 사전 분포에 사용할 수 있는 분포입니다.
• 확률 밀도 함수를 특징으로 하는 베타 분포
– 추정값과 오차 비율(평균과 분산)을 사용하여 베타 사전 분포를 지정합니다. 평균은 "추정값"에 입력한 값과 같고 분산은 (오차 비율/100 * 추정값)^2와 같습니다.
– 분포의 0.005 및 0.995 백분위수를 사용하여 베타 사전 분포를 지정합니다. JMP는 초모수를 취소합니다.