분포에 대한 통계 상세 정보

일반화 회귀 분석법에 의한 분포 적합은 모형 적합에 사용된 모수로 정의됩니다. 설명을 통해 구체적으로 언급되지는 않았지만 일반화 회귀 분석법을 사용하면 이산형 분포에 대해 정수가 아닌 값을 지정할 수 있습니다.

연속형 분포

정규 분포

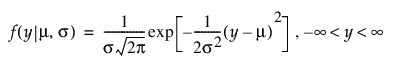
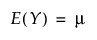
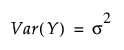
Cauchy 분포

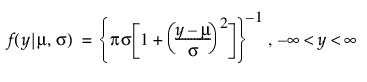
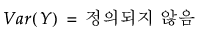
t(5) 분포

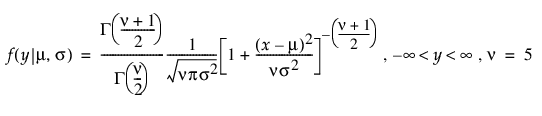
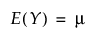
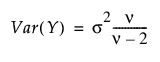
지수 분포

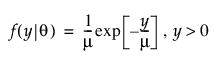
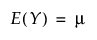
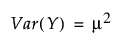
감마 분포

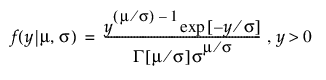
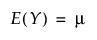
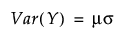
Weibull 분포

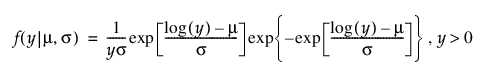
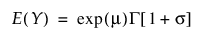
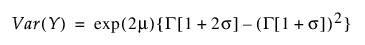
로그 정규 분포

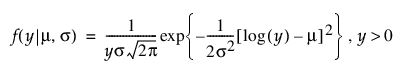
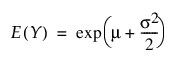
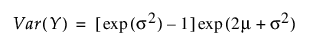
음의 로그 정규 분포

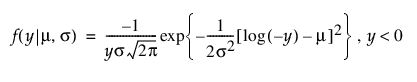
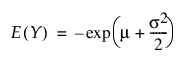
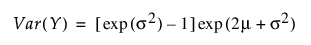
베타 분포

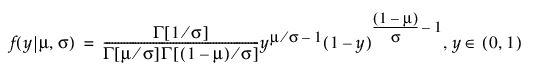
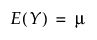
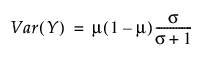
이산형 분포

이항 분포

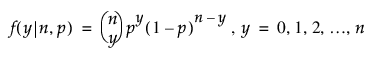
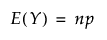
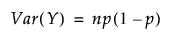
베타 이항 분포

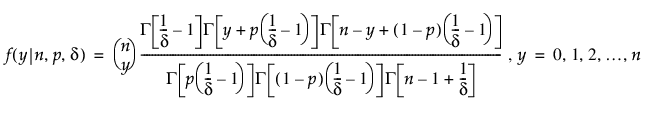
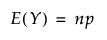
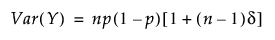
Poisson 분포

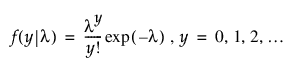
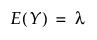
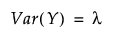
음이항 분포

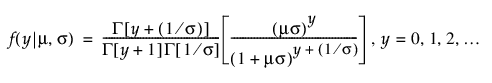
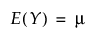
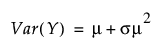
영과잉 분포

영과잉 이항 분포

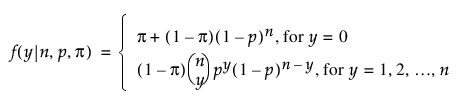
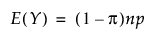
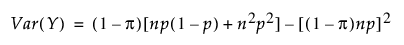
영과잉 베타 이항 분포

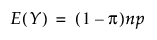
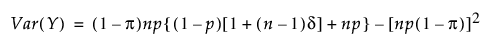
영과잉 Poisson 분포

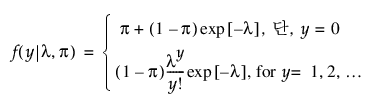
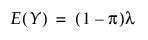
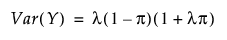
영과잉 음이항 분포

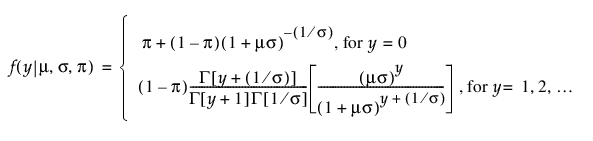
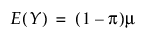
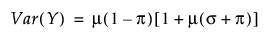
영과잉 감마 분포

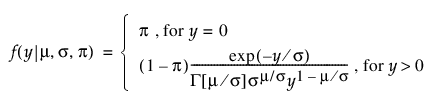
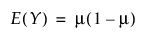
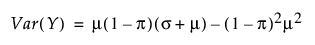
더 많은 정보를 원하십니까? 질문이 있습니까? JMP 사용자 커뮤니티에서 답변 받기 (community.jmp.com).