추정 방법에 대한 통계 상세 정보
모형 적합 플랫폼에서 일반화 회귀 분석법의 추정 방법에는 벌점을 적용하여 회귀 계수에 치우침을 적용하는 벌점 회귀 방법이 포함되어 있습니다.
능형 회귀
능형 회귀는 회귀 계수에 l2 벌점을 적용합니다. 능형 회귀 계수 추정값은 다음과 같이 정의됩니다.
,
여기서 
은 l2 벌점, l는 조정 모수, N은 행 수, p는 변수 수입니다.
Dantzig 선택기
Dantzig 선택기 방법은 잔차와 X 열의 내적에 l∞ 노름(norm)을 적용합니다. Dantzig 선택기에 대한 계수 추정값은 다음 기준을 충족합니다.
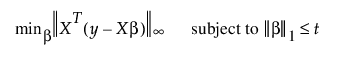
여기서 
은 l∞ 노름(norm)을 나타내고 
은 l1 벌점, t는 조정 모수입니다. l∞ 노름(norm)은 v 벡터 성분의 최대 절대값입니다.
Lasso 회귀
Lasso 회귀 방법은 회귀 계수에 l1 벌점을 적용합니다. Lasso 회귀의 계수 추정값은 다음과 같이 정의됩니다.
,
여기서 
는 l1 벌점, l는 조정 모수, N은 행 수, p는 변수 수입니다.
Elastic Net
Elastic Net 방법은 l1 벌점과 l2 벌점을 결합합니다. Elastic Net의 계수 추정값은 다음과 같이 정의됩니다.
,
다음은 방정식에 사용되는 표기입니다.
- l1 벌점
- l2 벌점
l - 조정 모수
a - l1 벌점과 l2 벌점의 결합을 결정하는 모수
N - 행 수
p - 변수 수
팁: Elastic Net에서 단일 예측 변수에 대한 가변 a 및 l의 축소 효과를 보여 주는 두 개의 샘플 스크립트가 있습니다. 도움말 > 샘플 인덱스를 선택하고, "샘플 인덱스"의 빨간색 삼각형을 클릭한, 다음, 샘플 열기 > 스크립트 선택하고 demoElasticNetAlphaLambda.jsl 또는 demoElasticNetAlphaLambda2.jsl을 선택합니다. 각 스크립트에는 스크립트 사용 방법 및 목적에 대한 설명이 포함되어 있습니다.
적응형 방법
적응형 Lasso 회귀 방법은 가중 벌점을 사용하여 일관된 계수 추정값을 제공합니다. l1 벌점의 가중 형식은 다음과 같이 정의됩니다.
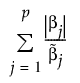
여기서 
는 MLE입니다(MLE가 있는 경우). MLE가 없고 반응이 정규 분포인 경우 최소 제곱을 사용하여 추정이 수행되고 
는 일반화 역행렬을 사용하여 구한 해입니다. 반응이 정규 분포가 아닌 경우 
는 능형 회귀 해입니다.
적응형 Lasso 회귀의 경우 이 가중 l1 벌점을 사용하여 
계수를 결정합니다.
적응형 Elastic Net은 이 가중 l1 벌점을 사용하고 가중 l2 벌점도 부과합니다. 적응형 Elastic Net에 대한 l2 벌점의 가중 형식은 다음과 같이 정의됩니다.
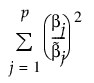
여기서 
는 MLE입니다(MLE가 있는 경우). MLE가 없고 반응이 정규 분포인 경우 최소 제곱을 사용하여 추정이 수행되고 
는 일반화 역행렬을 사용하여 구한 해입니다. 반응이 정규 분포가 아닌 경우 
는 능형 회귀 해입니다.