IRT 모형 적합에 대한 통계 상세 정보
항목 분석 플랫폼에서 항목 반응 이론 모형은 MMLE(주변 최대 가능도 추정)를 사용하여 적합됩니다. MMLE는 JLE(결합 최대 가능도 추정) 대신 사용할 수 있는 방법입니다. MMLE는 대상을 임의 효과로 처리합니다. 항목과 능력은 조건부 확률로 관련됩니다. 계산식은 다음과 같이 정의됩니다.
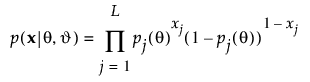
여기서 p(x|q, J)는 대상 능력 q와 항목 모수 벡터 J가 주어졌을 때 반응 벡터 x의 확률입니다. 항목 모수의 수는 사용된 모형(1PL, 2PL 또는 3PL)에 따라 다릅니다.
MMLE는 항목 모수 추정값을 얻기 위해 가우시안 구적을 사용하여 대상 효과를 통합합니다. 반응 벡터 x의 확률은 다음과 같이 계산됩니다.
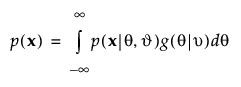
여기서 g(q|n)는 대상의 분포이고 n는 모집단 위치와 척도 모수의 벡터입니다. JMP에서는 평균이 0이고 표준편차가 1인 정규 분포가 g(q|n)에 사용됩니다.
참고: 테스트 질문에 대한 결측값은 올바르지 않은 반응으로 처리됩니다. 모두 올바르지 않게 답한 개인 또는 모두 올바르게 답한 개인에 대해서는 능력 스코어가 계산되지 않습니다. 이러한 대상에 대한 반응 패턴이 모형 추정에 포함됩니다.
IRT 모형 적합을 위한 MMLE 절차는 두 단계로 임의 효과 모형을 적합시키는 것과 비교할 수 있습니다. 능력 모수는 분산이 1인 임의 효과로 처리됩니다. 첫 번째 단계에서는 가우시안 구적을 사용하여 이러한 임의 효과가 통합됩니다. 항목 모수는 능력 모수가 통합된 상태에서 주변 가능도의 ML을 사용하여 추정되는 고정 효과로 처리됩니다. 능력 모수는 본질적으로 완전 비통합 (결합) 가능도를 사용하여 추정되는 최량 선형 비편향 예측입니다. 이때 항목 모수를 알려진 것으로 처리하고 첫 번째 단계에서 얻은 값으로 고정합니다.
L개 항목에 대한 2L 반응 패턴이 있습니다. 각 패턴의 능력 수준은 q가 수렴할 때까지 다음을 적용하여 반응 패턴에 대한 확률이 가장 높은 능력 수준을 찾는 방식으로 계산할 수 있습니다.
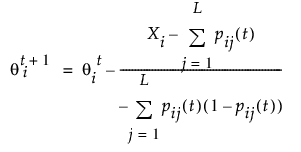
다음은 각 요소에 대한 설명입니다.
q = 반응 패턴을 얻을 가능도를 최대화합니다.
t = 반복 수
L = 항목 수
Xi = 관측된 스코어
pij = 항목 모수를 기반으로 i번째 사람이 j번째 항목에 대해 올바르게 반응할 확률