G 차트에 대한 통계 상세 정보

관리도 빌더에서 음이항 분포를 사용하여 G 차트의 시그마 값을 계산합니다. 음이항 분포는 기하(Poisson) 분포의 확장이며 Poisson과 관련하여 과대산포를 허용합니다. 음이항 분포를 사용하면 개수 데이터에 대해 정확 관리 한계와 근사 관리 한계를 모두 구성할 수 있습니다. 근사 관리 한계는 음이항에 대한 카이제곱 근사를 기반으로 구할 수 있습니다. 모든 데이터는 부분군 크기에 관계없이 개별 관측값으로 사용됩니다.

모수가 (m, k)인 음이항 분포의 X를 가정해 보겠습니다. 그러면 다음과 같이 구성할 수 있습니다.

다음은 각 요소에 대한 설명입니다.

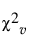= 자유도가 v = 2m/(1+mk)인 카이제곱 변량

이 근사를 기반으로 관리 상한 및 관리 하한의 근사값을 산출할 수 있습니다. 한 방향의 명목형 수준 a 제1종 오류 확률의 경우 근사 관리 상한은 다음 방정식이 참이 되는 한계(UCL)입니다.

마찬가지로 근사 LCL(관리 하한)은 다음 방정식이 참이 되는 한계입니다.

따라서 다음 계산식을 사용하여 근사 수준의 LCL(관리 하한) 및 UCL(관리 상한)이 계산됩니다.

다음은 각 요소에 대한 설명입니다.

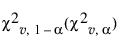= 자유도가 v = 2m/(1+mk)인 카이제곱 분포의 상위(하위) 백분위수. 음수 관리 하한은 0으로 설정할 수 있습니다.

음이항 관리 한계에 대한 자세한 내용은 Hoffman 연구 자료(2003)에서 확인하십시오.

더 많은 정보를 원하십니까? 질문이 있습니까? JMP 사용자 커뮤니티에서 답변 받기 (community.jmp.com).