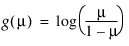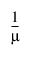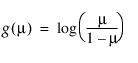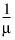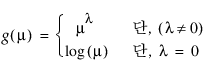일반화 선형 모형 생성에 대한 통계 상세 정보
일반화 선형 모형을 생성하려면 데이터에 대한 반응 변수와 설명 변수를 선택해야 합니다. 그런 다음 적절한 연결 함수와 반응 확률 분포를 선택해야 합니다. 설명 변수는 연속형 변수, 분류 변수 및 교호작용의 조합으로 지정할 수 있습니다. Table 13.1에는 일반화 선형 모형의 몇 가지 일반적인 예가 나열되어 있습니다.
|
모형 |
반응 변수 |
분포 |
기본 연결 함수 |
|---|---|---|---|
|
기존 선형 모형 |
연속형 |
정규 |
항등, g(m) = m |
|
로지스틱 회귀 |
개수 또는 이진 확률 변수 |
이항 |
로짓, |
|
로그 선형 모형의 Poisson 회귀 |
개수 |
Poisson |
로그, g(m) = log(m) |
|
지수 회귀 |
연속형 양수 |
지수 |
|
플랫폼에서 모수 벡터의 최대 가능도 추정을 통해 일반화 선형 모형을 데이터에 적합시킵니다. 일반적으로 모수의 최대 가능도 추정에 대한 닫힌 형식의 해는 없습니다. 따라서 이 플랫폼에서는 Nelder and Wedderburn 연구 자료(1972)에서 최초로 공개된 기법을 사용하여 반복 적합 프로세스를 통해 모형의 모수를 수치적으로 추정합니다. 과대산포 모수 f는 Pearson 적합도 통계량을 자유도로 나누어 추정합니다. 공분산, 표준 오차 및 신뢰 한계는 최대 가능도 추정량의 점근적 정규성을 기반으로 추정된 모수에 대해 계산됩니다.
모형 적합 플랫폼의 일반화 선형 모형 분석법에서 다양한 연결 함수 및 확률 분포를 사용할 수 있습니다. Table 13.2에는 기본 제공 연결 함수가 나열되어 있습니다.
|
연결 함수 이름 |
연결 함수 계산식 |
|---|---|
|
항등 |
g(m) = m |
|
로짓 |
|
|
프로빗 |
g(m) = F-1(m). F = 표준 정규 누적 분포 함수 |
|
로그 |
g(m) = log(m) |
|
역수 |
g(m) = |
|
거듭제곱 |
|
|
보 로그-로그 |
g(m) = log(–log(1 – m)) |
거듭제곱 연결 함수를 선택하면 원하는 검정력을 입력할 수 있는 숫자 상자가 나타납니다.
Table 13.3에는 반응 변수에 사용할 수 있는 분포와 관련된 분산 함수가 나열되어 있습니다.
|
분포 |
분산 함수 |
|---|---|
|
정규 |
V(m) = 1 |
|
이항 |
V(m) = m(1 – m) |
|
Poisson |
V(m) = m |
|
지수 |
V(m) = m2 |