한계에 대한 통계 상세 정보
모형 기반 다변량 관리도 플랫폼에서는 시작 창에 과거 행 수를 지정하지 않은 경우 모든 데이터가 과거 데이터로 처리됩니다. 자세한 내용은 모형 기반 다변량 관리도 플랫폼 시작에서 확인하십시오.
T2
과거 데이터의 UCL(관리 상한)은 베타 분포를 기반으로 하며 다음과 같이 정의됩니다.
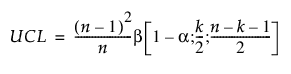
다음은 각 요소에 대한 설명입니다.
n = 과거 데이터 관측값 수
k = PCA 또는 PLS 성분 수
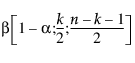= 베타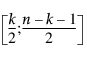
분포의 (1−a)번째 분위수
현재 데이터의 UCL은 F 분포를 기반으로 하며 다음과 같이 정의됩니다.
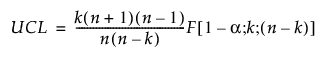
다음은 각 요소에 대한 설명입니다.
n = 과거 데이터 관측값 수
k = PCA 또는 PLS 성분 수
F(1−a; k; n−k) = F(k; n−k) 분포의 (1−a)번째 분위수
DModX
PCA 및 PLS 모형의 UCL은 F 분포를 기반으로 합니다. PCA 모형의 DModX UCL은 다음과 같이 정의됩니다.
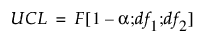
다음은 각 요소에 대한 설명입니다.
df1 = p−k
df2 = 데이터가 중심화된 경우 (n−k−1)(p−k), 데이터가 중심화되지 않은 경우 (n−k)(p−k)
n = 과거 데이터 관측값 수
k = PCA 성분 수
p = 변수 수
F(1−a; n−p−1; p−k) = F(n−p−1; p−k) 분포의 (1−a)번째 분위수
PLS 모형의 DModX UCL은 다음과 같이 정의됩니다.
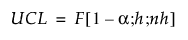
다음은 각 요소에 대한 설명입니다.
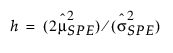
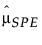= SPE의 과거 표본 평균
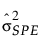= SPE의 과거 표본 분산
n = 과거 데이터 관측값 수
F(1−a; h; nh) = F(h; nh) 분포의 (1−a)번째 분위수
SPE
PCA 모형의 SPE UCL은 다음과 같이 정의됩니다.
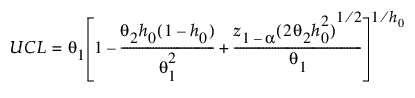
다음은 각 요소에 대한 설명입니다.
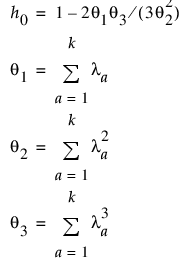
la = a번째 고유값
k = PCA 성분 수
z1−α = 표준 정규 분포의 (1−a)번째 분위수
PCA 모형의 SPE 관리 한계에 대한 자세한 내용은 Jackson and Mudholkar 연구 자료(1979)에서 확인하십시오.
PLS 모형의 UCL은 카이제곱 분포를 기반으로 하며 다음과 같이 정의됩니다.
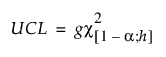
다음은 각 요소에 대한 설명입니다.
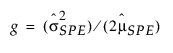
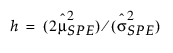
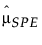= SPE의 과거 표본 평균
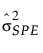= SPE의 과거 표본 분산
c2(1−a; h) = c2(h) 분포의 (1−a)번째 분위수
g 및 h 모수는 적률 방법으로 추정됩니다. PLS 모형의 SPE 관리 한계에 대한 자세한 내용은 Nomikos 연구 자료(1995)에서 확인하십시오.