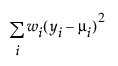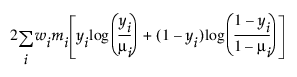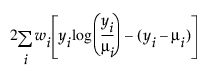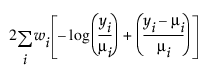모형 선택 및 이탈도에 대한 통계 상세 정보
일반화 선형 모델링의 중요한 특징은 모형의 설명 변수를 선택하는 것입니다. 적합도 통계량의 변화는 대개 설명 변수의 부분집합이 특정 모형에 미치는 기여도를 평가하는 데 사용됩니다. 이탈도는 도달 가능한 최대 로그 가능도와 회귀 모수의 최대 가능도 추정값에서의 로그 가능도 차이의 두 배로 정의됩니다. 이탈도는 주로 적합도의 측도로 사용됩니다. 도달 가능한 최대 로그 가능도는 모든 관측값에 대한 모수가 포함된 모형을 사용하여 얻을 수 있습니다. Table 13.4에는 반응 변수에 사용할 수 있는 각 분포에 대한 이탈도 계산식이 나열되어 있습니다.
|
분포 |
이탈도 계산식 |
|---|---|
|
정규 |
|
|
이항 |
|
|
Poisson |
|
|
지수 |
|
Pearson 카이제곱 통계량은 다음과 같이 정의됩니다.
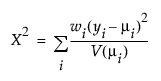
다음은 각 요소에 대한 설명입니다.
yi = i번째 반응
mi = 해당하는 예측 평균
V(mi) = 분산 함수
wi = i번째 관측값에 대한 알려진 가중치
참고: 가중치를 지정하지 않으면 모든 관측값에 대해 wi = 1입니다.
변수를 선택하는 한 가지 전략은 모형 시퀀스를 적합시키는 것입니다. 절편 항만 포함된 단순 모형으로 시작하여 각 연속 모형에 추가 설명 변수를 하나씩 포함합니다. 연속 모형 간의 이탈도 값이나 적합 로그 가능도 값의 차이로 추가 설명 변수의 중요도를 측정할 수 있습니다. 점근적 검정을 사용하면 추가 항의 통계적 유의성을 평가할 수 있습니다.
비정규 분포의 경우 역추정 예측에서 t 분포 임계값 대신 정규 임계값이 사용됩니다.
잔차 계산식
이탈도
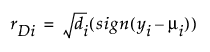
스튜던트화 이탈도
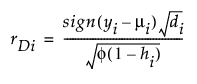
Pearson
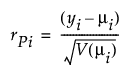
스튜던트화 Pearson
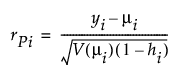
다음은 각 요소에 대한 설명입니다.
(yi – mi) = 원시 잔차
sign(yi – mi) = (yi – mi)가 양수인 경우 1, (yi – mi)가 음수인 경우 -1
di = 관측값 i의 총 이탈도에 대한 기여도
f = 산포 모수
V(mi) = 분산 함수
hi = We(1/2)X(X'WeX)-1X'We(1/2) 행렬의 i번째 대각 요소. 여기서 We는 기대 정보 행렬을 계산하는 데 사용되는 가중치 행렬입니다.
잔차 및 일반화 선형 모형에 대한 자세한 내용은 SAS Institute Inc. (2023a)의 "GENMOD Procedure" 장에서 확인하십시오.