부분 최소 제곱에 대한 통계 상세 정보
부분 최소 제곱은 요인, 즉 설명 변수(X)의 선형 결합을 기반으로 선형 모형을 적합시킵니다. 이러한 요인은 X와 하나 이상의 반응(Y) 간의 공분산을 최대화하는 방식으로 얻어집니다. 이런 식으로 PLS는 X와 Y 사이의 상관을 이용하여 기본 잠재 구조를 나타냅니다. 요인은 반응 변동과 예측 변수 변동을 설명해야 하는 합동 목표를 해결합니다. 부분 최소 제곱은 X 변수가 관측값보다 많거나 X 변수의 상관관계가 높을 때 특히 유용합니다.
NIPALS
NIPALS(Nonlinear Iterative Partial Least Squares) 방법은 한 번에 하나의 요인을 추출하는 방식으로 작동합니다. X = X0은 중심화 및 척도화된 예측 변수 행렬이고, Y = Y0은 중심화 및 척도화된 반응 값 행렬이라고 하겠습니다. PLS 방법은 예측 변수의 선형 결합인 t = X0w로 시작합니다. 여기서 t는 스코어 벡터이고 w는 연관된 가중치 벡터입니다. PLS 방법은 t에 대한 회귀 분석을 통해 X0과 Y0을 모두 예측합니다.
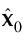= tp¢, 여기서 p´ = (t´t)-1t´X0
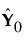= tc´, 여기서 c´ = (t´t)-1t´Y0
벡터 p와 c를 각각 X 및 Y 적재라고 합니다.
특정 선형 결합 t = X0w는 일부 반응 선형 결합 u = Y0q에서 최대 공분산 t´u를 갖는 결합입니다. 또 다른 특성은 X 및 Y 가중치를 나타내는 w와 q가 공분산 행렬 X0´Y0의 첫 번째 왼쪽 및 오른쪽 특이 벡터에 비례한다는 것입니다. 이는 X0´Y0Y0´X0과 Y0´X0X0´Y0의 첫 번째 고유 벡터에 각각 해당합니다.
이것은 첫 번째 PLS 요인이 추출되는 방법을 설명합니다. 두 번째 요인은 X0과 Y0을 첫 번째 요인의 X 및 Y 잔차로 대체하여 동일한 방식으로 추출됩니다.
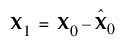
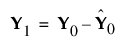
이러한 잔차를 수축된 X 및 Y 블록이라고도 합니다. 스코어 벡터 추출 및 데이터 행렬 수축 과정이 추출된 요인 수만큼 반복됩니다.
SIMPLS
SIMPLS(Statistically Inspired Modification of Partial Least Squares) 알고리즘은 통계 기준을 최적화하기 위해 개발되었습니다. 이 방법은 X 스코어가 직교해야 한다는 요건에 따라 X와 Y의 선형 결합 간에 공분산을 최대화하는 스코어 벡터를 찾습니다. X0 및 Y0 행렬이 수축되는 NIPALS와 달리 SIMPLS는 교차곱 행렬 X0´Y0을 수축시킵니다.
단일 Y 변수의 경우 이 두 알고리즘이 동일합니다. 그러나 다변량 Y의 경우 모형이 다릅니다. SIMPLS는 De Jong(1993)에 의해 제안되었습니다.