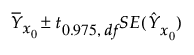예측 및 신뢰 한계에 대한 통계 상세 정보
이 섹션에서는 부분 최소 제곱 플랫폼에서 예측 및 신뢰 한계의 표준 오차 계산에 대해 설명합니다. X를 예측 변수 행렬로 나타내고 Y를 반응 값 행렬로 나타냅니다. 이러한 값은 시작 창에서 선택한 항목에 따라 중심화 및 척도화될 수 있습니다. Y의 성분은 공통 분산이 s2인 독립 정규 분포를 따른다고 가정합니다.
Hoskuldsson(1988)은 Y에 대한 PLS 모형을 스코어 관점으로 보면 다중 선형 회귀 모형과 형식적으로 유사하다는 것을 발견했습니다. 또한 이 유사성을 사용하여 예측값의 분산에 대한 근사 계산식을 도출했습니다. Umetrics(1995) 연구 자료도 확인하십시오. 그러나 Denham(1997)은 PLS에 의해 예측된 값은 Y의 비선형 함수임을 지적했습니다. 또한 예측 구간을 얻기 위해 붓스트랩 및 교차 검증 기법을 제안했습니다. PLS 플랫폼에서는 Umetrics(1995)에 설명된 정규성 기반 방식을 사용합니다.
열에 스코어가 포함된 행렬을 T로 나타내고 X의 새 관측값 x0을 예로 들어보겠습니다. Y에 대한 예측 모형은 T를 기반으로 Y를 모델링하는 회귀를 통해 얻습니다. x0과 관련된 스코어 벡터를 t0으로 나타냅니다.
a가 요인 수를 나타낸다고 하겠습니다. s2을 df = n - a -1(데이터가 중심화된 경우) 및 df = n - a(데이터가 중심화되지 않은 경우)로 나눈 잔차 제곱합으로 정의합니다. s2 값은 s2의 추정값입니다.
예측 계산식의 표준 오차
x0에서 예측 평균의 표준 오차는 다음과 같이 추정됩니다.
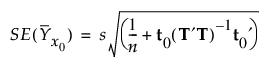
평균 신뢰 한계 계산식
t0.975, df를 자유도가 df = n - a -1(데이터가 중심화된 경우) 및 df = n - a(데이터가 중심화되지 않은 경우)인 t 분포의 0.975 분위수를 나타낸다고 하겠습니다.
평균에 대한 95% 신뢰 구간은 다음과 같이 계산됩니다.
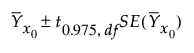
개별값 신뢰 한계 계산식
x0에서 예측된 개별 반응의 표준 오차는 다음과 같이 추정됩니다.
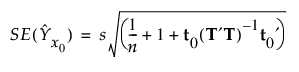
t0.975, df를 자유도가 df = n - a -1(데이터가 중심화된 경우) 및 df = n - a(데이터가 중심화되지 않은 경우)인 t 분포의 0.975 분위수를 나타낸다고 하겠습니다.
개별 반응에 대한 95% 신뢰 구간은 다음과 같이 계산됩니다.