적합 요약 측도에 대한 통계 상세 정보
이 섹션에서는 구조 방정식 모형 플랫폼에 보고되는 적합 요약 측도에 대해 설명합니다.
AICc, BIC 및 BICu
AICc 및 BIC는 다음과 같이 정의됩니다.
AICc =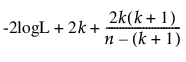 
BIC =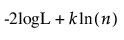 
다음은 각 요소에 대한 설명입니다.
-2logL = 음의 로그 가능도의 두 배
n = 표본 크기
k = 모수 수
"모형 비교" 보고서의 가능도 기반 측도에 대한 자세한 내용은 선형 모형 적합의 가능도, AICc 및 BIC에서 확인하십시오.
BICu(제약 없는 모형에 대한 BIC)는 다음과 같이 정의됩니다.
BICu =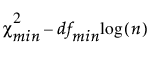 
다음은 각 요소에 대한 설명입니다.
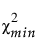= 적합 모형의 카이제곱 통계량
dfmin = 적합 모형의 자유도
n = 표본 크기
적합 모형의 BICu는 적합 모형의 BIC에서 제약 없는 모형의 BIC를 뺀 값과 같습니다. 제약 없는 모형의 BIC에 대한 자세한 내용은 Bollen et al. (2014)에서 확인하십시오.
CFI
CFI(비교 적합 지수)는 다음과 같이 정의됩니다.
CFI =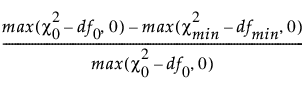 
다음은 각 요소에 대한 설명입니다.
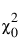= 독립 모형의 카이제곱 통계량
df0 = 독립 모형의 자유도
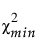= 적합 모형의 카이제곱 통계량
dfmin = 적합 모형의 자유도
CFI에 대한 자세한 내용은 Bentler(1990) 연구 자료에서 확인하십시오.
RNI
RNI(상대 비중심성 지수)는 다음과 같이 정의됩니다.
RNI =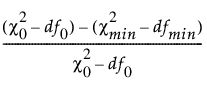 
다음은 각 요소에 대한 설명입니다.
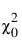= 독립 모형의 카이제곱 통계량
df0 = 독립 모형의 자유도
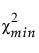= 적합 모형의 카이제곱 통계량
dfmin = 적합 모형의 자유도
RNI에 대한 자세한 내용은 McDonald & Marsh(1990)에서 확인하십시오.
TLI
TLI(Tucker-Lewis 지수)는 다음과 같이 정의됩니다.
TLI =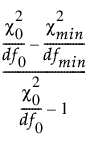 
다음은 각 요소에 대한 설명입니다.
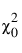= 독립 모형의 카이제곱 통계량
df0 = 독립 모형의 자유도
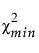= 적합 모형의 카이제곱 통계량
dfmin = 적합 모형의 자유도
자세한 내용은 West et al. (2012) 연구 자료에서 확인하십시오.
NFI
Bentler-Bonett NFI(표준 적합 지수)는 다음과 같이 정의됩니다.
NFI =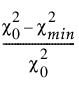 
다음은 각 요소에 대한 설명입니다.
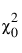= 독립 모형의 카이제곱 통계량
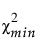= 적합 모형의 카이제곱 통계량
자세한 내용은 West et al. (2012) 연구 자료에서 확인하십시오.
수정 GFI 및 수정 AGFI
수정 GFI(수정 적합도 지수)는 다음과 같이 정의됩니다.
수정 GFI =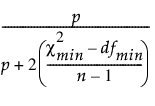 
다음은 각 요소에 대한 설명입니다.
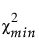= 적합 모형의 카이제곱 통계량
dfmin = 적합 모형의 자유도
p = 적합 모형에서 관측 변수의 수
n = 표본 크기
수정 AGFI(수정 조정 적합도 지수)는 다음과 같이 정의됩니다.
수정 AGFI =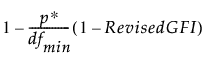 
다음은 각 요소에 대한 설명입니다.
p* = 공분산 행렬 및 관측 변수 평균 벡터의 고유 항목 수
dfmin = 적합 모형의 자유도
자세한 내용은 Maiti & Mukherjee(1991) 및 West et al. (2012)에서 확인하십시오.
RMSEA
RMSEA(근사의 제곱근 평균 제곱 오차)는 다음과 같이 정의됩니다.
RMSEA =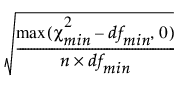 
다음은 각 요소에 대한 설명입니다.
n = 표본 크기
dfmin = 적합 모형의 자유도
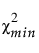= 적합 모형의 카이제곱 통계량
RMSEA에 대한 신뢰 한계는 비중심 카이제곱 분포 F(x|l, d)의 누적 분포 함수를 사용하여 계산됩니다. 90% 신뢰 한계는 다음과 같이 계산됩니다.
하한 =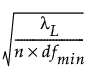 
상한 =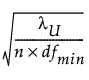 
다음은 각 요소에 대한 설명입니다.
lL은 F(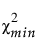
|lL, dfmin) = 0.95를 충족합니다.
lU는 F(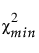
|lU, dfmin) = 0.05를 충족합니다.
자세한 내용은 Maydeu-Olivares et al. (2017)에서 확인하십시오.
RMR 및 SRMR
RMR 및 SRMR 계산식은 다음과 같이 정의됩니다.
RMR =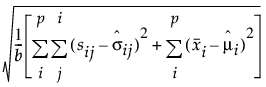 
SRMR =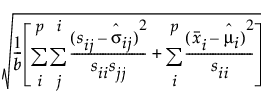 
다음은 각 요소에 대한 설명입니다.
p = 명시 변수의 수
b = 공분산 행렬 및 관측 변수 평균 벡터의 고유 항목 수
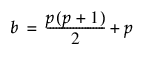
sij = 입력 공분산 행렬의 (i, j)번째 요소
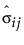= 예측 공분산 행렬의 (i, j)번째 요소
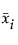= 표본 평균 벡터의 i번째 요소
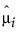= 예측 평균 벡터의 i번째 요소
자세한 내용은 SAS Institute Inc. (2023a)의 "CALIS Procedure" 장에서 확인하십시오.