수렴 스코어 검정에 대한 통계 상세 정보
"혼합 모형" 보고서에서 수렴 실패 경고는 알 수 없는 MLE(최대 가능도 추정값)가 모형 적합 알고리즘의 최종 반복에서 제공된 모수와 일치한다는 가설에 대한 스코어 검정을 보여 줍니다. 이 가설 검정은 상대 그래디언트 기준이 스코어 검정 통계량과 대수적으로 동등하므로 가능합니다. 또한 스코어 검정에는 실제 MLE에 대한 정보가 필요 없습니다.
스코어 검정
먼저 단일 모수 q를 가정해 보겠습니다. l을 q의 로그 가능도 함수로 하고 x를 데이터로 합니다. 스코어는 다음과 같이 q에 대한 로그 가능도 함수의 도함수입니다.
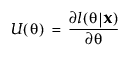
관측된 정보:
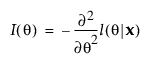
H0: q = q0의 스코어 검정에 대한 통계량:
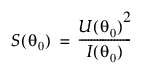
이 통계량은 귀무가설 하에서 자유도가 1인 점근적 카이제곱 분포를 따릅니다.
스코어 검정을 여러 모수로 일반화할 수 있습니다. 모수 q의 벡터를 가정해 보겠습니다. H0: q = q0의 스코어 검정에 대한 통계량은 다음과 같습니다.
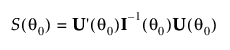
여기서,
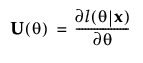
및
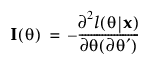
U¢는 U 행렬의 전치를 나타냅니다.
검정 통계량은 자유도가 k인 점근적 카이제곱 분포입니다. 여기서 k는 비유계 모수의 수입니다.
상대 그래디언트
혼합 모형 적합 절차의 수렴 기준은 상대 그래디언트 g¢H−1g를 기반으로 합니다. 여기서 g(q) = U(q)는 로그 가능도 함수의 그래디언트이고, H(q) = -I(q)는 헤시안 행렬입니다.
q0을 알고리즘이 종료되는 q의 값이라고 하겠습니다. q0 에서 평가된 상대 그래디언트가 스코어 검정 통계량입니다. p 값은 자유도가 k인 카이제곱 분포를 사용하여 계산됩니다. 이 p 값은 알 수 없는 MLE 값이 q0와 일치하는지 여부를 나타냅니다. "임의 효과 공분산 모수 추정값" 보고서에 나열된 비유계 모수의 수는 k입니다.