Crow-AMSAA 보고서에 대한 통계 상세 정보
이 섹션에는 "Crow-AMSAA" 보고서에 표시되는 모수 추정값 및 프로파일러에 대한 상세 정보가 포함되어 있습니다.
Crow-AMSAA 모형의 모수 추정값
"수정된 MLE를 포함하는 Crow-AMSAA" 옵션을 제외하고 l 및 b의 추정값은 다음과 같이 계산되는 최대 가능도 추정값입니다. 가능도 함수는 Meeker & Escobar(1998)의 방법론을 사용하여 도출됩니다. 이는 param1 = log(l) 및 param2 = log(b)에 따라 다시 파라미터화됩니다. 이 작업은 무제약 최적화 알고리즘, 즉 -∞에서 +∞까지 검색하는 알고리즘을 사용할 수 있도록 하기 위해 수행됩니다. param1 및 param2에 대한 MLE를 얻습니다.
l 및 b의 표준 오차는 Fisher 정보 행렬에서 얻습니다. param1 및 param2에 대한 신뢰 한계는 Wald 통계량을 사용하여 MLE의 점근 분포를 기반으로 계산됩니다. 이러한 추정값과 신뢰 한계는 지수 함수를 사용하여 원래 단위로 다시 변환됩니다.
수정된 MLE를 포함하는 Crow-AMSAA의 모수 추정값
"수정된 MLE를 포함하는 Crow AMSAA" 옵션의 경우 b 추정값은 편향이 수정됩니다. b의 편향 수정 추정값 계산식은 시험이 고장 종료되었는지 아니면 시간 종료되었는지에 따라 달라집니다.
b에 대한 MLE를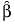 
로 나타내고 n은 관측값 수, T는 총 시험 시간이라고 하겠습니다.
b의 편향 수정 추정값(수정된 MLE)은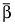 
입니다.
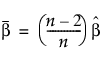고장 종료된 시험의 경우
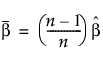시간 종료된 시험의 경우
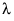에 대한 수정된 MLE(
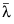로 표시)는 가능도 함수로 주어진 표현식에 따라 계산되지만 조정된 베타 값을 기반으로 합니다.
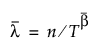
모수에 대한 공분산 행렬은 Fisher 정보 행렬을 사용하여 추정됩니다. 자세한 내용은 Crow-AMSAA 모형의 모수 추정값에서 확인하십시오. 그러나 l 및 b의 편향 수정 추정값이 결과 계산식의 MLE 대신 사용됩니다. 그림의 모든 신뢰 대역과 보고서의 신뢰 구간은 이 절차를 기반으로 합니다.
프로파일러
Crow-AMSAA 모형의 경우 프로파일러에 제공된 MTBF, 강도 및 누적 사건에 대한 추정값은 이론적 표현식의 l 및 b 모수를 MLE로 대체하여 계산됩니다. "수정된 MLE를 포함하는 Crow-AMSAA" 옵션의 경우 수정된 MLE가 사용됩니다. 신뢰 한계는 관심 표현식의 로그에 델타 방법을 적용하여 구합니다.
누적 사건 함수를 예로 들어보겠습니다. 시험 시작 이후 시간 t에서의 누적 사건 수는 N(t) = ltβ로 지정됩니다. 따라서 log(N(t)) = log(l) + blog(t)입니다. log(N(t))의 l 및 b 모수는 log(N(t))를 추정하기 위해 MLE 또는 수정된 MLE로 대체됩니다. 델타 방법이 이 표현식에 적용되어 분산 추정값을 구합니다. 이 추정값은 95% Wald 기반 신뢰 구간을 생성하는 데 사용됩니다. 그런 다음 지수 함수를 사용하여 결과 신뢰 한계가 변환되고 시간 t에서의 추정된 누적 사건 수에 대한 신뢰 한계를 제공합니다.