직교 적합 옵션에 대한 통계 상세 정보

이변량 플랫폼에서 "직교 적합" 옵션을 사용하여 수직 차이의 제곱합을 최소화하는 선을 적합시킬 수 있습니다. X 측정값에 랜덤 변동이 있는 경우 표준 최소 제곱보다 이 방법을 사용하는 것이 좋습니다. 표준 최소 제곱 적합은 X 변수가 고정되어 있고 Y 변수가 X + 오차의 함수라고 가정합니다.

참고: 수직 거리는 X 및 Y의 척도화 방법에 따라 달라지며, 수직 거리의 척도화는 그래픽 문제가 아니라 통계적 문제로 남아 있습니다.

그림 5.22 적합선에 수직인 선 

적합을 수행하려면 X의 오차 분산에 대한 Y의 오차 분산의 비율을 지정해야 합니다. 이는 표본 점의 분산이 아니라 오차의 분산이므로 신중하게 선택해야 합니다. 표준 최소 제곱에서는 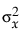이 0이기 때문에 비율이 무한대가 됩니다. 오차 비율이 큰 직교 적합은 표준 최소 제곱 적합선에 가까워집니다. 비율을 0으로 지정하면 X에 대한 Y가 아니라 Y에 대한 X의 회귀와 동등한 적합이 수행됩니다.

이 방법의 가장 일반적인 용도는 동일한 값을 측정하는 데 오차가 있는 두 측정 시스템을 비교하는 것입니다. 따라서 Y 반응 오차와 X 측정 오차가 모두 동일한 유형의 측정 오차입니다. 오차 비율은 1(등분산)과 같이 가정된 값이거나, 측정 시스템에 대한 지식을 기반으로 할 수 있습니다.

신뢰 한계는 Tan and Iglewicz 연구 자료(1999)에 설명된 것과 같이 계산됩니다.