다중 요인 분석 플랫폼에 대한 통계 상세 정보
다중 요인 분석은 하위 테이블의 정보를 테이블 행의 항목을 설명하는 일련의 직교 열로 결합합니다. 기본 절차는 다음과 같습니다.
• 각 하위 테이블에서 PCA를 수행합니다.
• 각 하위 테이블의 첫 번째 고유값을 기록하여 가중치 행렬을 생성합니다.
• 하위 테이블을 나란히 연결하고 행렬을 중심화 및 정규화합니다.
• 연결된 테이블에서 특이값 분해를 통해 일반화 PCA를 수행합니다. 일반화 PCA는 하위 테이블 가중치를 사용하여 해를 제한하는 데 사용됩니다.
이 결과 일반화된 오른쪽 및 왼쪽 특이 벡터와 특이값의 세 가지 행렬이 생성됩니다. 그런 다음 이를 사용하여 하위 테이블의 컨센서스에 대한 성분 스코어, 고유값 및 성분 적재를 도출합니다. 이 세 가지 행렬은 원래 측정값의 많은 열을 측정 대상 개체 사이의 유사성 및 차이를 설명하는 해석 가능한 몇 가지 차원으로 분해한 결과입니다.
계산
MFA의 경우 X 행렬의 특이값 분해를 다음과 같이 정의할 수 있습니다.
, 
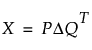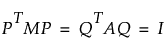제약 조건 사용
사용되는 행렬은 다음과 같습니다.
X는 하위 테이블의 중심화 및 정규화된 n x p 행렬입니다. 소비자 조사의 경우 n개의 제품과 p개의 참가자 평가가 있습니다.
Q는 q개의 주성분에 대한 적재를 얻기 위해 MFA 특이값에 의해 가중치가 부여된 오른쪽 특이 벡터의 p x q 행렬입니다.
D는 일반화 PCA에서 얻은 특이값의 q x q 대각 행렬입니다. PCA와 마찬가지로 특이값 제곱 또는 고유값의 크기는 결합 분석에서 각 주성분의 중요도를 나타냅니다.
P는 q개의 절충 주성분을 얻기 위해 MFA 특이값에 의해 가중치가 부여된 왼쪽 특이 벡터의 n x q 행렬입니다.
M은 질량 가중치의 n x n 대각 행렬입니다.
A는 블록 또는 참가자 가중치의 p x p 대각 행렬입니다.
다중 요인 분석에 대한 자세한 내용은 Abdi et al. (2013)에서 확인하십시오.
질량 가중치
JMP 계산에서는 질량 가중치 계산에 N - 1을 사용합니다. 이러한 계산은 개별 스코어와 블록 부분 스코어에 영향을 줍니다.