스트레스 함수에 대한 통계 상세 정보

다차원 척도법 플랫폼에서는 MDS 좌표를 결정하기 위해 quasi-Newton 최적화 방법을 사용하여 스트레스 함수를 최소화합니다. 이 최소화로 인해 차원의 각 쌍별 집합에 대해 도출된 근접성 측도를 최소화하는 좌표 집합이 미리 결정된 수의 차원에 생성됩니다. 데이터가 순서형이면 단조 회귀가 사용됩니다. 그렇지 않으면 표준 최소 제곱 회귀가 사용됩니다.

다음 표기를 사용하여 스트레스를 정의합니다.

• i, j - 개체 수에 대한 인덱스

• dij - 개체 i와 j 사이의 유도 거리

dij - 개체 i와 j 사이의 관측된 상대 거리

• f(drs) - 거리에 대한 변환 함수

스트레스 함수는 다음과 같이 정의됩니다.

스트레스 =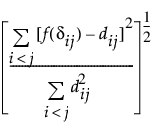

이 스트레스 측도는 Kruskal 스트레스, 제1종 또는 간단히 스트레스 1이라고도 합니다.

더 많은 정보를 원하십니까? 질문이 있습니까? JMP 사용자 커뮤니티에서 답변 받기 (community.jmp.com).