다차원 척도법

개체 집합 간의 근접성 시각화

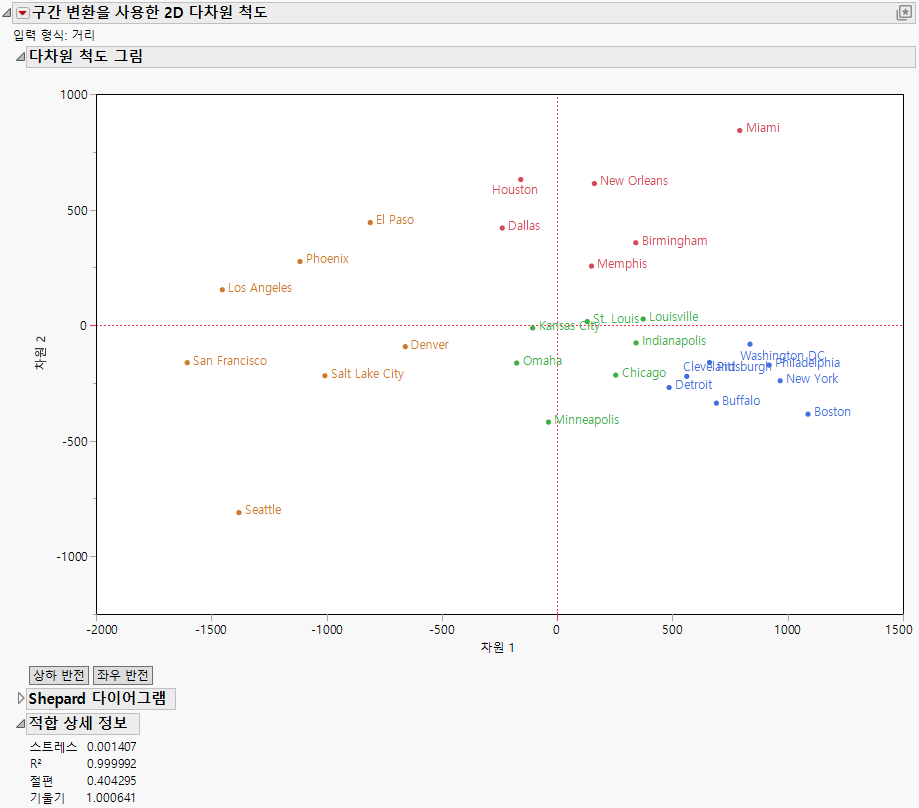
MDS(다차원 척도법)는 개체 집합 간의 근접성 패턴(유사성, 비유사성 또는 거리)을 시각적으로 표현하는 데 사용되는 기법입니다. 예를 들어 도시 간의 거리 행렬이 주어진 경우 MDS를 사용하여 2차원 도시 맵을 생성할 수 있습니다.

다차원 척도법은 연구원이 브랜드, 취향 또는 기타 상품 속성과 관련된 인식 측도를 가지고 있는 소비자 조사에 주로 사용됩니다. MDS는 근접성 또는 속성 집합을 기반으로 개체의 근접성을 시각화하는 데 관심이 있는 다른 많은 분야에 적용할 수 있습니다.

그림 10.1 다차원 척도법의 예 

목차

다차원 척도법 플랫폼 개요

다차원 척도법의 예

다차원 척도법 플랫폼 시작

다차원 척도 보고서

다차원 척도 그림

Shepard 다이어그램

적합 상세 정보

다차원 척도법 플랫폼 옵션

Waern 링크

다차원 척도법의 추가 예

다차원 척도법 플랫폼에 대한 통계 상세 정보

스트레스 함수에 대한 통계 상세 정보

변환에 대한 통계 상세 정보

속성 목록 형식에 대한 통계 상세 정보